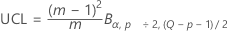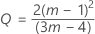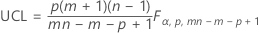请选择您所选的方法或公式。
标绘点
子组中的数据
当数据位于子组中时, T2 的计算方法如下:

其中:
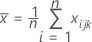
 是
是 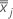 的均值向量(xjk
值的均值),其计算方式如下:
的均值向量(xjk
值的均值),其计算方式如下:
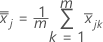
S = 样本协方差矩阵
样本协方差矩阵 S 的计算方式如下:

其中:
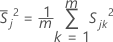
其中:
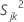 ,第 k个样本中第 j个 特征的样本方差计算如下:
,第 k个样本中第 j个 特征的样本方差计算如下:
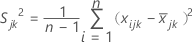
其中:
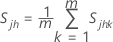
其中:
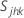 ,是协方差,=
,是协方差,=
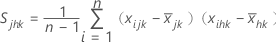
S 矩阵的平均值是当过程受控制时方差的无偏估计值。n 必须大于 p ,并且变量之间不得有强关联,以便样本协方差矩阵不是奇异阵。
当数据位于子组中时,图表将显示作为单个观测值的任何子组的缺失值。
单个观测值
当数据是单个观测值时, T2 的计算方法如下:

其中:
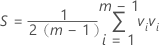
其中:

表示法
| 项 | 说明 |
|---|---|
| n | 样本数量 |
 | 样本均值向量 |
| xijk | 第 k个 样本中 第 j个 特征的第 i个 观测值 |
| m | 样本数 |
T2 的计算示例
Minitab 在控制图上标绘 T2 统计量。如果标绘点超出控制限,则过程在该点不受控制。有关 Minitab 计算的参考,请参见相关表格和样本方程。
下面的数据来自一个清洁液开发过程。柠檬酸钠和甘油的含量将影响清洁液的效力。
| 子组均值 | 方差和协方差 | T2 统计量 | ||||
| 子组 | 柠檬酸钠 (X1) | 甘油 (X2) | S 1 2 | S2 2 | S 1 2 k | T2 |
| 1 | 125 | 025 | 7292 | 8692 | 5791 | 5708 |
| 2 | 625 | 4 | 2292 | 2333 | 3333 | 1429 |
| 3 | 4 | 875 | 1467 | 0625 | 8000 | 9528 |
| 4 | 2 | 2 | 2933 | 7600 | 6667 | 8073 |
| 5 | 25 | 225 | 2500 | 2692 | 7917 | 7548 |
| 6 | 4 | 45 | 6667 | 9567 | 3333 | 2711 |
| 7 | 275 | 025 | 3692 | 4692 | 7108 | 7785 |
| 8 | 6 | 65 | 4333 | 7700 | 6933 | 6183 |
| 9 | 625 | 325 | 7892 | 5558 | 1325 | 3592 |
| 10 | 3 | 5 | 2867 | 9467 | 2600 | 4942 |
| 11 | 25 | 5 | 1767 | 1200 | 9000 | 3279 |
| 12 | 1 | 625 | 1467 | 1692 | 4033 | 0277 |
| 平均值 | 7875 | 2333 | 7931 | 9318 | 3003 | |
- 为每个变量(X1 和 X2)计算子组均值。在这种情况下,每个子组都有四个样本。
- 如果有单个观测值,Minitab 会在所有计算中使用这些值来取代子组均值。
- 计算子组方差 S1 2 和 S2 2.
- 计算子组协方差 S1 2 k.
- 计算子组均值的均值、子组方差的均值和协方差的均值。
- 指定样本协方差矩阵 S 和均值向量。
- 计算 T2,其计算方式如下:
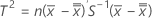
Minitab 在 T2 控制图上标绘 T2,并将它与控制限相比较以确定单个点是否不受控制。
中心线
T2 控制图的中心线是 KX。K 和 X 的计算取决于最大样本数量以及 Minitab 是否根据数据估计协方差矩阵。
子组中的数据
当数据位于子组中时,KX 的计算方式如下:
- 给定的协方差矩阵
-


- 估计的协方差矩阵
-


单个观测值
当数据是单值观测值时,KX 按如下方式计算:
- 给定的协方差矩阵
-
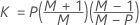
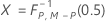
- 估计的协方差矩阵
-
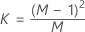
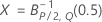
其中:
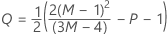
表示法
| 项 | 说明 |
|---|---|
| P | 变量数 |
| M | 子组数 |
| N | 样本数量 |
 | 分子自由度为 u 分母自由度为 v 的逆累积 F 分布 |
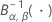 | 第一个分布形状参数和第二个分布形状参数分别为 α 和 β 的逆累积 beta 分布 |
控制限
子组中的数据
未指定参数时的控制上限为:
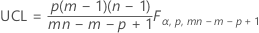
指定了参数时的控制上限为:
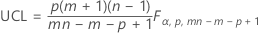
表示法
| 项 | 说明 |
|---|---|
| αα | 固定值为 0.00134989803156746 |
| p | 特征数 |
| m |
对于子组中的数据,如果未指定参数估计值,则 m 是样本的数量。如果您明确提供了参数估计值,则 m 是用来创建协方差矩阵的样本数量。 对于单值数据,m 是观测值的个数。 |
| n | 每个样本的大小 |
| F | 指示所使用的是 F 分布 |
| B | 指示所使用的是 beta 分布 |
分解的 T 方统计量
分解的 T 方统计量:
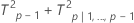
其中:

其中:
xi(p − 1) 是分解的均值向量
Sxx 是 S 的 (p – 1) × (p – 1) 主子矩阵
T2p|1,..., p−1 是一个近似值,它因所处的阶段以及您拥有的是子组还是单个观测值而异。
子组中数据的阶段 1:
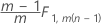
子组中数据的阶段 2:
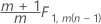
单个观测值的阶段 1:
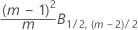
单个观测值的阶段 2:
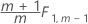
当您未指定参数估计值时,Minitab 计算阶段 1 的控制限;当您指定了参数估计值时,Minitab 计算阶段 2 的控制限。
有关分解的 T 方统计量的更多信息,请参见 Mason 等人发表的 2。
表示法
| 项 | 说明 |
|---|---|
| m | 样本数 |
| F | 指示所使用的是 F 分布 |
| B | 指示所使用的是 beta 分布 |
Box-Cox 的方法和公式
Box-Cox 公式
如果您使用 Box-Cox 变换,Minitab 根据以下公式变换原始数据值 (Yi):
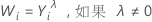
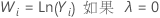
其中 λ 是变换参数。Minitab 随后创建变换数据值 (Wi) 的控制图。要了解 Minitab 如何为 λ 选择最优值,请转到Box-Cox 变换 的方法和公式。
常见的 λ 值
| λ | 变换 |
|---|---|
| 2 | 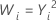 |
| 0.5 |  |
| 0 |  |
| −0.5 | 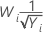 |
| −1 | 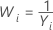 |