Pp
可以使用您指定的参数值计算 Pp,也可以使用分析中所用分布的极大似然法估算 Pp。Minitab 使用Z 值法(默认)或ISO 方法估算 Pp 统计量,具体方法取决于在中选择的设置。以下公式基于 K = 6 的默认公差,公差宽度是 6 个标准差(过程均值的每一侧有 3 个标准差)。
Z 值法

表示法
| 项 | 说明 |
|---|---|
| Zlsl | Φ–1(p1) |
| Zusl | Φ–1(p2) |
| Φ–1(p) | p * 标准正态分布的第 100 个百分位数 |
| p1 | Prob (X ≤ LSL) |
| P2 | Prob (X ≤ USL) |
| X | X 服从分析中所使用的分布 |
ISO 方法

表示法
| 项 | 说明 |
|---|---|
| USL | 规格上限 |
| LSL | 规格下限 |
| X.99865 | 指定分布的第 .99.865 个百分位数 |
| X.00135 | 指定分布的第 .135 个百分位点 |
Ppk

预期整体性能所对应的合计 PPM
超出规格限制的预期百万分数的计算方式如下:
PPM Total (Exp. Overall) = PPM < LSL (Exp. Overall) + PPM > USL(Exp. Overall)
PPM Total (Exp. Overall) = [1,000,000 * F(LSL)]+ [1,000,000 * (1 – F(USL))]
表示法
| 项 | 说明 |
|---|---|
| F(X) | 在基于估计或指定参数的分析中使用的标准正态分布的累积分布函数 (CDF) |
| LSL | 规格下限 |
| USL | 规格上限 |
| PPM | 百万分数 |
基准 Z 值 Z.LSL Z.USL
通过使用标准正态 (0,1) 分布查找对应统计量的 Z 值,计算出整体能力的基准 Z 值统计量。


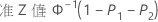
注意
PPL 和 PPU 基于此分析中使用的方法(ISO 或 Minitab)。有关更多信息,请转到在 非正态能力分析 中用于度量整体能力的方法和公式。以下公式基于 K = 6 的默认公差,公差宽度是 6 个标准差(过程均值的每一侧有 3 个标准差)。
表示法
| 项 | 说明 |
|---|---|
| P1 | 概率(观测值 < LSL)基于分析中使用的非正态分布和您指定的参数(或者根据数据估计的参数) |
| P2 | 概率(观测值 > USL)基于分析中使用的非正态分布和您指定的参数(或者根据数据估计的参数) |
| Φ (X) | 标准正态分布的累积分布函数 (CDF) |
| Φ–1 (X) | 标准正态分布的逆 CDF |
