In This Topic
Kendall's coefficient of concordance
Use Kendall's statistic with ordinal data of three or more levels.
In the description of the method, without loss of generality, we assume that a single rating on each subject is made by each rater, and there are k raters per subject. Then, to calculate Kendall's coefficient, the k raters represent the k trials for each rater.
Suppose data are arranged into a k x N table with each row representing the ranks assigned by a particular rater to the N subjects.
Formulas
When the true standard is not known, Minitab estimates Kendall's coefficient by:
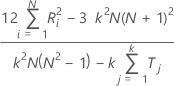
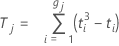
Notation
| Term | Description |
|---|---|
| N | the number of subjects |
| Σ Ri2 | the sum of the squared sums of ranks for each of the ranked N subjects |
| K | the number of appraisers |
| Tj | Tj assigns the average of ratings to tied observation |
| Term | Description |
|---|---|
| ti | the number of tied ranks in the ith grouping of ties |
| gj | the number of groups of ties in the jth set of ranks |
Testing significance of Kendall's coefficient of concordance
To test the significance of Kendall's coefficient, use:
c 2= k (N – 1) W
Notation
| Term | Description |
|---|---|
| c 2 | is distributed as chi-square with N – 1 degrees of freedom |
| k | the number of appraisers |
| N | the number of subjects |
| W | the calculated Kendall's coefficient |
Kendall's correlation coefficient
Use Kendall's statistic with ordinal data of three or more levels.
In the description of the method, without loss of generality, we assume that a single rating on each subject is made by each rater, and there are k raters per subject. Then, to calculate Kendall's correlation coefficient, the k raters represent the k trials made by all the raters.
When the true standard is known, Minitab estimates Kendall's correlation coefficient by calculating the average of the Kendall's coefficients between each appraiser and the standard.
The Kendall's correlation coefficient for the agreement of the trials with the known standard is the average of the Kendall correlation coefficients across trials.
Formulas
Minitab calculates Kendall's coefficient between each trial and the standard using:

Notation
| Term | Description |
|---|---|
| TX | number of pairs tied on X = 0.5 Σi ni+ (ni+– 1) |
| TY | number of pairs tied on Y = 0.5 Σj n+j (n+j– 1) |
| C | number of concordant pairs = Σi<kΣj<l nij nkl |
| D | number of discordant pairs = Σi<kΣj>l nij nkl |
| Term | Description |
|---|---|
| ni+ | number of observations in the ith row |
| n+j | number of observations in the jth column |
| nij | observations in the cell corresponding to ith row and jth column |
| nkl | observations in the cell corresponding to kth row and lth column |
| n++ | total number of observations |
Reference
A. Agresti (1984). Analysis of Ordinal Categorical Data, John Wiley & Sons.
Testing significance of Kendall's correlation coefficient
Formula
To test the significance of Kendall's coefficient when the true standard is known, use:
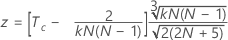
use:
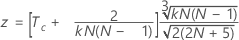
Notation
| Term | Description |
|---|---|
| Tc | the average of the Kendall correlation coefficients between each appraiser and the standard |
| N | the total number of subjects |
| k | the number of raters |
