Select the method or formula of your choice.
In This Topic
Coefficient (Coef)
In matrix terms, the formula that calculates the vector of coefficients in the model is:

Notation
| Term | Description |
|---|---|
| X | design matrix |
| Y | response vector |
Standard error of the coefficient (SE Coef)
The standard errors of the coefficients for multiple regression are the square roots of the diagonal elements of this matrix:
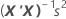
Notation
| Term | Description |
|---|---|
| X | design matrix |
| X' | transpose of the design matrix |
| s2 | mean square error |
T-value
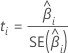
Notation
| Term | Description |
|---|---|
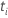 | test statistic for the 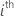 coefficient coefficient |
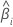 | 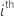 estimated coefficient estimated coefficient |
 | standard error of the 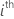 estimated coefficient estimated coefficient |
P-value – Coefficients table
The two-sided p-value for the null hypothesis that a regression coefficient equals 0 is:
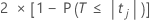
The degrees of freedom are the degrees of freedom for error, as follows:
n – p – 1
Notation
| Term | Description |
|---|---|
 | The cumulative distribution function of the t distribution with degrees of freedom equal to the degrees of freedom for error. |
| tj | The t statistic for the jth coefficient. |
| n | The number of observations in the data set. |
| p | The sum of the degrees of freedom for the terms. The terms do not include the constant. |
