Use the exponential distribution to model the time between events in a continuous Poisson process. It is assumed that independent events occur at a constant rate.
This distribution has a wide range of applications, including reliability analysis of products and systems, queuing theory, and Markov chains.
- How long it takes for electronic components to fail
- The time interval between customers' arrivals at a terminal
- Service time for customers waiting in line
- The time until default on a payment (credit risk modeling)
- Time until a radioactive nucleus decays
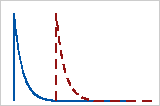
For the 1-parameter exponential distribution, the threshold is zero, and the distribution is defined by its scale parameter. For the 1-parameter exponential distribution, the scale parameter equals the mean.
What does memoryless mean?
An important property of the exponential distribution is that it is memoryless. The chance of an event does not depend on past trials. Therefore, the occurrence rate remains constant.
The memoryless property indicates that the remaining life of a component is independent of its current age. For example, random trials of a coin toss demonstrate the memoryless property. A system that has wear and tear, and thus becomes more likely to fail later in its life, is not memoryless.
