CART always uses the average of two adjacent values to calculate c. A continuous variable with N distinct values generates up to N–1 potential splits of the parent node. In an analysis, the actual number of potential splits is smaller when the minimum node size is greater than 1.
For a categorical variable X with distinct values {c1, c2, c3, ..., ck}, a split is a subset of levels which are sent to the left node. A categorical variable with k levels generates up to 2k – 1-1 splits.
For a potential split during the tree growing phase, the criteria for improvement is either Least Squares (LS) or Least Absolute Deviation (LAD). Minitab adds the split with the highest improvement to the tree. If the improvement for two predictors is the same, the algorithm requires a selection to proceed. The selection uses a deterministic tie-breaking scheme that involves the position of the predictors in the worksheet, the type of predictor, and the number of classes in a categorical predictor.
Minitab calculates improvements only from the training data when the analysis includes a model validation method. Use the following formulas to calculate the improvement for each criterion.
Least Squares (LS)

where

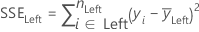

Least Absolute Deviation (LAD)

where

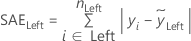

Notation
| Term | Description |
|---|---|
| SSE | sum of squared errors |
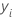 | ith record in the node |
| SAE | sum of the absolute errors |
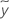 | median of the response for the node |
Surrogate splits
After the identification of an optimal split, Minitab looks for surrogate splits among the other potential splits. A surrogate split resembles the optimal split in which records go to the left and right nodes. The measure of resemblance is association.
An association of 1 indicates that the surrogate split replicates the optimal split. An association of 0 indicates that the split sends all records to the node with more records in the optimal split. Splits with positive association are potential surrogates. Improvements from surrogate splits are in the calculations of variable importance.
When new data include missing values for any of the predictors that form splits, Minitab uses the best non-missing surrogate predictor instead of the predictor that appears in the tree.
