Design matrix
First, Minitab creates a design matrix from the factors and the model that you specify. The columns of this matrix represent the terms in the model. Then, Minitab adds additional columns for the constant term, blocks, and higher-order terms to complete the design matrix for the model in the analysis.
Designs with all continuous factors
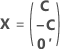
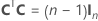
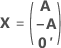
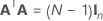
The full design matrix contains columns besides the columns that represent factors. The design matrix contains a column of 1s for the constant term. The full design matrix also includes columns that represent any square or interaction terms in the model.
Designs with categorical factors
For a design that includes categorical factors, Minitab replaces the single center point row in the design matrix with 2 pseudo center points. If the design has only 1 categorical factor, only two possible pseudo center points exist, so both points are in the design.
In the case where the design has more than 2 categorical factors, Minitab uses an iterative algorithm to select 2 pseudo center points to include. The algorithm seeks to minimize the variance of the regression coefficients for the linear effects in the model.
Notation
| Term | Description |
|---|---|
| C | A conference matrix |
| 0' | A row of zeroes in a matrix that represent a center point run |
| In | the n × n identity matrix |
| A | A matrix that is a subset of a conference matrix with N rows and n columns where  |
| N | The number of rows in the subset of the columns from the conference matrix |
| n | The number of factors in a design |
Coefficient (Coef)
In matrix terms, the formula that calculates the vector of coefficients in the model is:

Notation
| Term | Description |
|---|---|
| X | design matrix |
| Y | response vector |
Box-Cox transformation
Box-Cox transformation selects lambda values, as shown below, which minimize the residual sum of squares. The resulting transformation is Y λ when λ ≠ 0 and ln(Y) when λ = 0. When λ < 0, Minitab also multiplies the transformed response by −1 to maintain the order from the untransformed response.
Minitab searches for an optimal value between −2 and 2. Values that fall outside of this interval might not result in a better fit.
Here are some common transformations where Y′ is the transform of the data Y:
| Lambda (λ) value | Transformation |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0.5 | Y′ = 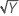 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0.5 |  |
| λ = −1 | Y′ = −1 / Y |
Weighted regression
Weighted least squares regression is a method for dealing with observations that have nonconstant variances. If the variances are not constant, observations with:
- large variances should be given relatively small weights
- small variances should be given relatively large weights
The usual choice of weights is the inverse of pure error variance in the response.
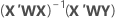

Notation
| Term | Description |
|---|---|
| X | design matrix |
| X' | transpose of the design matrix |
| W | an n x n matrix with the weights on the diagonal |
| Y | vector of response values |
| n | number of observations |
| wi | weight for the ith observation |
| yi | response value for the ith observation |
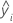 | fitted value for the ith observation |
