In This Topic
Probability Plots
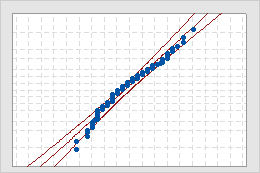
- Middle line
- The expected percentile from the distribution based on maximum likelihood parameter estimates.
- Confidence bound lines
- The left curved line indicates the lower bounds of the confidence intervals for the percentiles. The right curved line indicates the upper bounds of the confidence intervals for the percentiles.
- Anderson-Darling test statistic and p-value
- The results of a test to determine whether your data follow the distribution.
Interpretation
Use the probability plots to assess the fit of the nonnormal distribution for each variable.
If the distribution is a good fit for the data, the points should form an approximately straight line. Departures from this straight line indicate that the fit is unacceptable. If the p-value is greater than 0.05, you can assume that the data follow the nonnormal distribution used in the analysis.
Note
If the distributions differ for multiple variables, you should perform a separate capability analysis for each variable.
Capability Histogram
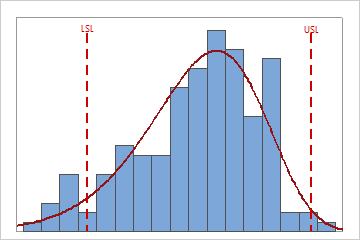
Interpretation
Use the capability histogram to view your sample data in relation to the distribution fit and the specification limits.
- Look for evidence of lack-of-fit of your selected nonnormal data distribution
-
For each variable, compare the distribution curve to the bars of the histogram to assess whether your data seem to follow the distribution that you chose for the analysis. If the bars vary greatly from the curve, your data may not follow your chosen distribution and the capability estimates may not be reliable for your process. If you are unsure which distribution best fits your data, use Individual Distribution Identification to identify an appropriate distribution or transformation.
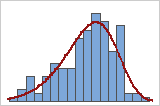
Good fit
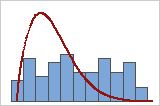
Poor fit
Important
The histograms provide only a rough indication of the distribution fit. To more definitively assess the distribution fit, use the results on the probability plots. If the distributions differ for multiple variables, you should perform a separate capability analysis for each variable.
- Examine the sample data in relation to the specification limits
- For each variable, visually examine the data in the histogram in relation to the lower and upper specification limits. Ideally, the spread of the data is narrower than the specification spread, and all the data are inside the specification limits. Data that are outside the specification limits represent nonconforming items. Ideally, few or no parts are outside of the specification limits.
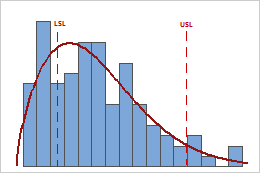
In these results, the process spread is larger than the specification spread, which suggests poor capability. Although much of the data are within the specification limits, there are many nonconforming items below the lower specification limit (LSL) and above the upper specification limit (USL).
Note
To determine the actual number of nonconforming items in your process, use the results for PPM < LSL, PPM > USL, and PPM Total. For more information, go to All statistics and graphs.
- Assess the location of the process
-
For each variable, evaluate whether the process is centered between the specification limits or at the target value, if you have one. The peak of the distribution curve shows where most of the data are located.
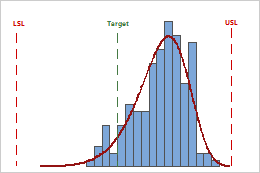
In these results, although the sample observations fall inside of the specification limits, the peak of the distribution curve is not on the target. Most of the data exceed the target value and are located near the upper specification limit.
