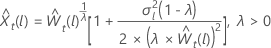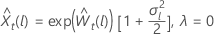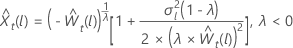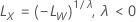Previsão com o melhor modelo ARIMA compara muitos modelos e seleciona um modelo final com um critério nas especificações da análise. Para obter informações sobre os resultados do modelo ARIMA final, acesse Métodos e fórmulas para ARIMA. As seções a seguir contêm detalhes exclusivos de Previsão com o melhor modelo ARIMA.
Seleção do modelo
A seleção do modelo utiliza as seguintes etapas:
- Estime os parâmetros do modelo para cada modelo. Se um modelo inclui uma constante e a estimativa dos parâmetros falha, tente estimar os parâmetros sem o termo constante.
- Calcule o critério de informação para cada modelo. O critério padrão é o Critério de Informação Akaike (AICc) corrigido.
- Produzir resultados para o modelo com o melhor valor do critério de informação.
As seções a seguir descrevem detalhes que diferem na seleção de modelos não sazonais e sazonais.
Modelos não sazonais
- Quando você encaixa modelos com um termo constante, os modelos candidatos têm p + q ≤ 9.
- Quando você encaixa modelos sem um termo constante, os modelos candidatos têm p + q ≤ 10.
- Modelos com d = 2 nunca incluem um termo constante.
- O modelo avalia ARIMA(0, d, 0) somente quando d = 1.
Modelos sazonais
- Quando você encaixa modelos com um termo constante, os modelos candidatos têm p + q + P + Q ≤ 9.
- Quando você encaixa modelos sem um termo constante, os modelos candidatos têm p + q + P+ Q ≤ 10.
- Modelos com d + D > 1 nunca incluem um termo constante.
- A busca por um modelo sazonal requer a ordem de pelo menos um dos parâmetros sazonais para ser maior que 0. A pesquisa inclui modelos não sazonais se as especificações da pesquisa incluem modelos onde todos os parâmetros sazonais têm pedidos de 0.
- Pelo menos 1 de p, q, P e Q não é zero em todos os modelos.
Critério
- Critério de Informação de Akaike (AIC)
- Critério de informação de Akaike corrigido (AICc)
- Critério de Informação bayesiana (BIC)
O cálculo dos critérios de informação para um modelo utiliza o valor de probabilidade de log para o modelo. O cálculo do valor de probabilidade de registro usa um algoritmo recursivo. Para obter mais informações, consulte a seção 8.6 de Brockwell & Davis (1991)1.
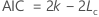
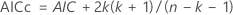

Notação
| Termo | Descrição |
|---|---|
| k | o número de parâmetros no modelo
|
| Lc | a log-verossimilhança do modelo atual |
| n | o tamanho amostral da série temporais |
Transformação de Box-Cox
A análise permite uma transformação Box-Cox dos dados. A transformação dos dados acontece antes da seleção do modelo. Para obter informações sobre a transformação Box-Cox para dados de séries tempores, acesse Métodos e fórmulas para Transformação de Box-Cox para séries temporais.
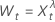 para λ > 0
para λ > 0 para λ = 0
para λ = 0 para λ < 0
para λ < 0
em que 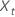 é o valor tth da série temporal original e t = 1, ..., n.
é o valor tth da série temporal original e t = 1, ..., n.
Seja 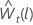 ser o valorl th previsão a partir da origem, t, para os dados transformados. Seja
ser o valorl th previsão a partir da origem, t, para os dados transformados. Seja  ser a variância de previsão l-passo a partir dos dados transformados. Em seguida, o valorde previsão l de t para a série original depende do valor de λ:
ser a variância de previsão l-passo a partir dos dados transformados. Em seguida, o valorde previsão l de t para a série original depende do valor de λ:
em que  é o limite na escala original e
é o limite na escala original e 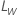 é o limite na escala transformada.
é o limite na escala transformada.
Modelo de caminhada aleatório
O modelo ARIMA(0, 1, 0), com ou sem termo constante, é o modelo de caminhada aleatório. Em Minitab Statistical Software, Previsão com o melhor modelo ARIMA se encaixa no modelo de caminhada aleatória. O comando requer pelo menos um parâmetro médio autoregressivo ou móvel. Os limites de estimativa e probabilidade para o modelo de caminhada aleatória têm formas específicas. Os cálculos para a loglikelihood, os limites de previsão e os limites de probabilidade para as previsões dependem se o modelo inclui um termo constante.
Definições:
| Termo | Descrição |
|---|---|
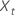 | as observações para uma série temporal com t = 1, ..., n |
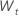 | os primeiros dados diferentes da série temporais original,  |
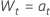
ou
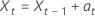
em que 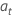 são distribuídos de forma independente e idêntica e seguem a distribuição normal com média 0 e variância σ2, t = 2, ..., n.
são distribuídos de forma independente e idêntica e seguem a distribuição normal com média 0 e variância σ2, t = 2, ..., n.
Equações que representam o modelo com uma constante são semelhantes:

ou
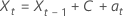

Modelo sem termo constante
A loglikelihood tem a seguinte forma:
Loglikelihood
em que
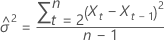

O limite de probabilidade de 100 × (1 – α) para o valor da previsão 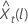 tem a seguinte forma:
tem a seguinte forma:
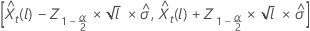
em que  representa os 100 × (1 – α/2)º percentil da distribuição normal padrão.
representa os 100 × (1 – α/2)º percentil da distribuição normal padrão.
Modelo com termo constante
Para um modelo com uma constante, os cálculos para a loglikelihood requerem a estimativa da constante, C. Primeiro, diferença os dados da série original 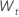 para t = 2, ..., n. A constante é a média amostral de
para t = 2, ..., n. A constante é a média amostral de 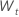 tem a seguinte forma:
tem a seguinte forma:
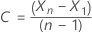
A loglikelihood tem a seguinte forma:
Loglikelihood
em que
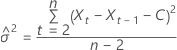
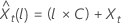
O limite de probabilidade de 100 × (1 – α) para o valor da previsão 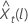 tem a seguinte forma:
tem a seguinte forma:
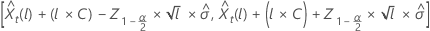
em que  representa os 100 × (1 – α/2)º percentil da distribuição normal padrão.
representa os 100 × (1 – α/2)º percentil da distribuição normal padrão.