Neste tópico
Etapa 1: Determinar se a linha de regressão se ajusta aos seus dados
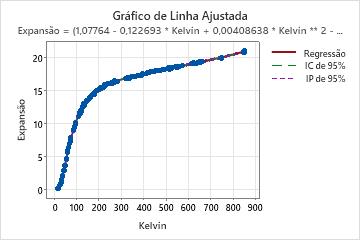
Se seu modelo não linear contém apenas um preditor, o Minitab exibe o gráfico de linha ajustada para mostrar a relação entre os dados de resposta e do preditor. O gráfico inclui a linha de regressão, que representa a equação de regressão. Você também pode escolher exibir os intervalos de confiança de 95% e de predição no gráfico.
- A amostra contém um número adequado de observações ao longo de toda a faixa de todos os valores de predição.
- O modelo ajusta adequadamente qualquer curvatura aos dados. Para determinar qual modelo é melhor, examine o gráfico, o erro padrão da regressão (S) e o teste de ajuste (lack-of-fit) quando os seus dados contiverem repetições.
- Procure por todos os outliers, os quais podem exercer forte efeito sobre os resultados. Tente identificar a causa de qualquer outliers. Corrija os erros de entrada de dados ou de medição. Considere a remoção de valores de dados que estejam associados a eventos anormais que ocorrem somente uma vez (causas especiais). Em seguida, repita a análise. Para obter mais informações sobre detecção de outliers, vá para Observações atípicas.
Etapa 2: Examinar a relação entre as preditoras e a resposta
Use a equação de regressão, para descrever a relação entre a resposta e os termos no modelo. A equação de regressão é uma representação algébrica da linha de regressão. Insira o valor de cada preditor na equação para calcular o valor médio de resposta. Ao contrário de regressão linear, de uma equação de regressão não linear pode ter muitas formas.
Para equações não lineares, determinar do efeito que cada preditor exerce sobre a resposta pode ser menos intuitivo do que para equações lineares. Ao contrário das estimativas dos parâmetros em modelos lineares, não há nenhuma interpretação consistente para as estimativas de parâmetros em modelos não lineares. A interpretação correta para cada parâmetro depende da função de expectativa e do lugar do parâmetro nele. Se seu modelo não-linear contém apenas um preditor, avalie o gráfico de linha ajustada para ver a relação entre o preditor e a resposta.
Se for necessário determinar se uma estimativa de parâmetros é estatisticamente significativa, use os intervalos de confiança para os parâmetros. O parâmetro é estatisticamente significativo se o intervalo exclui o valor da hipótese nula. O Minitab não pode calcular os valores de p para parâmetros em regressão não linear. Para regressão linear, o valor da hipótese nula para cada parâmetro é zero, para nenhum efeito, e o valor de p é baseado neste valor. No entanto, na regressão não linear, o valor correto da hipótese nula para cada parâmetro depende da função de expectativa e do lugar do parâmetro nele.
Para alguns conjuntos de dados, funções expectativa e níveis de confiança, é possível um ou ambos os limites de confiança deixem de existir. O Minitab indica resultados ausentes com um asterisco. Se o intervalo de confiança tiver um limite faltante, um nível de confiança inferior pode produzir um intervalo bilateral.
A convergência em uma solução não garante necessariamente que o modelo de ajuste é ideal ou que a soma dos quadrados dos erros (SSE) é minimizada. A convergência em valores de parâmetros incorretos pode ocorrer devido a um SSE local mínimo ou a uma função de expectativa incorreta. Portanto, é essencial examinar os valores dos parâmetros, gráfico de linha ajustada e gráficos de resíduos, para determinar se o modelo de ajuste de parâmetros e valores são razoáveis.
Equação
3) / (1 - 0,00576099 * Kelvin + 0,000240537 * Kelvin ** 2 - 1,23144E-07 * Kelvin ** 3)
Resultado principal: Equação
Nestes resultados, existe um preditor e sete estimativas de parâmetros. A variável de resposta é Expansão e a variável preditora é a temperatura na escala Kelvin. A equação longa descreve a relação entre a resposta e os preditores. O efeito que o aumento de 1 grau Kelvin tem sobre a expansão do cobre depende fortemente da temperatura inicial. O efeito das mudanças de temperatura sobre a expansão de cobre não pode ser facilmente resumido. Avalie o gráfico de linha ajustada para ver a relação entre o preditor e a resposta.
Se você inserir um valor para a temperatura em Kelvin na equação, o resultado é o valor ajustado para a expansão do cobre.
Etapa 3: Determinar quão bem o modelo se ajusta aos seus dados
Para determinar quão bem o modelo se ajusta aos seus dados, examine as estatísticas na tabela Resumo do modelo e na tabela Falta de ajuste.
- S
-
Use S para avaliar se o modelo descreve bem a resposta.
S é medido nas unidades da variável de resposta e representa o quão longe os valores de dados caem dos valores ajustados. Quanto mais baixo for o valor de S, melhor o modelo descreve a resposta. No entanto, um valor de S baixo por si só não indica que o modelo satisfaz aos pressupostos do modelo. Você deve verificar os gráficos de resíduos para conferir os pressupostos.
- Falta de ajuste
-
O Minitab exibe automaticamente a tabela Falta de ajuste quando seus dados contêm réplicas. As réplicas são múltiplas observações com valores de preditora idênticos. Se os seus dados não contêm réplicas, é impossível calcular o erro puro que é necessário para executar este teste. Os valores de resposta diferentes para as réplicas representam o erro puro, pois apenas a variação aleatória pode causar diferenças entre os valores de resposta observados.
Para determinar se o modelo especifica corretamente a relação entre a resposta e os preditores, compare o valor-p para o teste de ajuste (lack-of-fit) com o seu nível de significância para avaliar a hipótese nula. A hipótese nula para o teste de ajuste (lack-of-fit) é que o modelo especifica corretamente a relação entre a resposta e os preditores. Em geral, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Um nível de significância de 0,05 indica um risco de 5% de concluir que o modelo não especifica corretamente a relação entre a resposta e os preditores quando o modelo não especifica a relação correta.- Valor-p ≤ α: o teste de ajuste (lack-of-fit) é estatisticamente significativo
- Se o valor-p for menor ou igual ao nível de significância, conclua que o modelo não especifica corretamente a relação. Para melhorar o modelo, talvez seja necessário adicionar termos ou transformar seus dados.
- Valor-p ≤ α: o teste de ajuste (lack-of-fit) não é estatisticamente significativo
-
Se o valor-p for maior do que o nível de significância, o teste não detecta nenhum teste de ajuste (lack-of-fit).
Falta de Ajuste
| Fonte | GL | SQ | QM | F | P |
|---|---|---|---|---|---|
| Erro | 229 | 1,53244 | 0,0066919 | ||
| Falta de Ajuste | 228 | 1,52583 | 0,0066922 | 1,01 | 0,679 |
| Erro puro | 1 | 0,00661 | 0,0066125 |
Sumário
| Iterações | 15 |
|---|---|
| SQE Final | 1,53244 |
| GLE | 229 |
| MSE | 0,0066919 |
| S | 0,0818039 |
Principais resultados: S, Falta de ajuste
Nesses resultados, S indica que o desvio padrão da distância entre os valores de dados e os valores ajustados é de aproximadamente 0,08 unidades. O valor-p para o teste de falta de ajuste é de 0,679, o que não fornece evidências de que o modelo se ajusta mal aos dados.
Etapa 4: Determinar se o modelo atende às suposições da análise
Use os gráficos de resíduos para ajudar a determinar se o modelo é adequado e satisfaz aos pressupostos da análise. Se os pressupostos não forem satisfeitos, o modelo pode não ajustar bem os dados e você deve ter cautela ao interpretar os resultados.
Para obter mais informações sobre como lidar com os padrões nos gráficos residuais, vá para Gráficos de resíduos para Regressão não-linear e clique no nome do gráfico residual na lista na parte superior da página.
Gráficos de resíduos versus de ajustes
Use o gráfico de resíduos versus ajustes para verificar a pressuposição de que os resíduos são aleatoriamente distribuídos e têm variância constante. De maneira ideal, os pontos devem cair aleatoriamente em ambos os lados de 0, sem padrões reconhecíveis nos pontos.
| Padrão | O que o padrão pode indicar |
|---|---|
| Dispersão grande ou irregular de resíduos entre valores ajustados | Variância não constante |
| Curvilíneo | Um termo de ordem mais alta ausente |
| Um ponto que está distante de zero | Um outlier |
| Um ponto que é distante dos outros pontos na direção x | Um ponto influente |
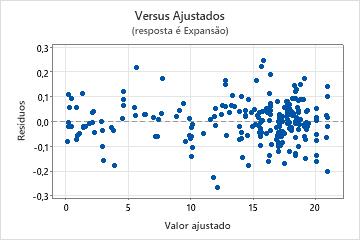
Gráfico de resíduos versus ordem
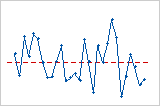
Tendência
Deslocamento
Ciclo
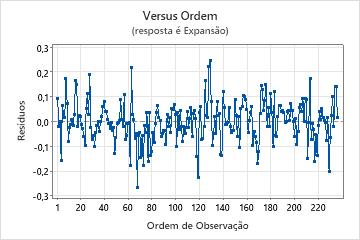
Gráficos de probabilidade normal de resíduos
Use o gráfico de probabilidade normal de resíduos para verificar a pressuposição de que os resíduos são distribuídos normalmente. O gráfico de probabilidade normal dos resíduos deve seguir aproximadamente uma linha reta.
| Padrão | O que o padrão pode indicar |
|---|---|
| Não é uma linha reta | Não normalidade |
| Um ponto que está distante da linha | Um outlier |
| Alteração de inclinação | Uma variável não identificada |