Ajuste
Valores ajustados são também chamados de ajustes ou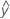 
. Os valores ajustados são estimativas pontuais de a resposta média para determinados valores dos preditores. Os valores dos preditores também são chamados valores de x.
Interpretação
Valores ajustados são calculados inserindo os valores x específicos para cada observação no conjunto de dados para o modelo da equação.
Por exemplo, se a equação for y = 5 + 10x, o valor ajustado para o valor de x, 2, é 25 (25 = 5 + 10(2)).
As observações com valores ajustados que são muito diferentes do valor observado pode ser incomuns. As observações com valores de preditor incomuns podem ser influentes. Se o Minitab determinar que os dados incluem valores incomuns ou influentes, a saída inclui a tabela de tabela Ajustes e Diagnósticos para Observações Incomuns, que identifica essas observações. As observações que o Minitab rotula como incomuns não seguem bem a equação de regressão proposta. No entanto, espera-se que você tenha algumas observações incomuns. Por exemplo, com base nos critérios de grandes resíduos padronizados, espera-se que aproximadamente 5% das observações sejam sinalizadas como tendo um grande resíduo padronizados. Para obter mais informações sobre valores incomuns, acesse Observações atípicas.
Ajuste SE
O erro padrão do ajuste (EP fit) estima a variação na resposta da média estimada para as configurações de variável especificadas. O cálculo do intervalo de confiança para a resposta média usa o erro padrão do ajuste. Os erros padrão são sempre não negativos.
Interpretação
Use o erro padrão do ajuste para medir a exatidão da estimativa da resposta média. Quanto menor o erro padrão, mais precisa é a resposta média predita. Por exemplo, um analista desenvolve um modelo para predizer o tempo de entrega. Para um conjunto de configurações de variável, o modelo prediz um tempo de entrega médio de 3,80 dias. O erro padrão do ajuste para estas configurações é 0,08 dias. Para o segundo conjunto de configurações de variáveis, o modelo produz o mesmo tempo de entrega médio, com um erro padrão de ajuste de 0,02 dias. O analista pode ter mais confiança de que o tempo médio de entrega para o segundo conjunto de configurações de variáveis está próximo de 3,80 dias.
Com o valor ajustado, é possível usar o erro padrão do ajuste para criar um intervalo de confiança para a resposta média. Por exemplo, dependendo do número de graus de liberdade, um intervalo de confiança de 95% se estende cerca de dois desvios padrão acima e abaixo da média prevista. Para os tempos de entrega, o intervalo de confiança de 95% para a média prevista de 3,80 dias, quando o erro padrão é de 0,08 é (3,64, 3,96) dias. Você pode ter 95% de confiança de que a média da população está dentro deste intervalo. Quando o erro padrão é de 0,02, o intervalo de confiança de 95% é (3,76, 3,84) dias. O intervalo de confiança para o segundo conjunto de definições de variáveis é mais estreito, porque o erro padrão é menor.
IC de 95%
O intervalo de confiança do ajuste fornece um intervalo de valores prováveis para a resposta média dadas as configurações especificadas das preditoras.
Interpretação
Use o intervalo de confiança para avaliar a estimativa do valor ajustado para os valores observados das variáveis.
Por exemplo, com um nível de confiança de 95%, você pode ter 95% de confiança de que o intervalo de confiança contém a média da população para os valores especificados das variáveis no modelo. O intervalo de confiança ajuda a avaliar a significância prática de seus resultados. Use seu conhecimento especializado para determinar se o intervalo de confiança inclui valores que tenham significância prática para a sua situação. Um amplo intervalo de confiança indica que você pode estar menos confiante sobre a média de valores futuros. Se o intervalo for muito amplo para ser útil, pense em aumentar o tamanho da amostra.
PI de 95%
O intervalo de predição é um intervalo que provavelmente contém uma única resposta futura para um valor de variável da preditora dadas as configurações especificadas das preditoras.
Interpretação
Por exemplo, um engenheiro de materiais em uma fábrica de móveis desenvolve um modelo de regressão simples para predizer a rigidez de uma placa de aglomerado a partir da densidade da placa. O engenheiro verifica se o modelo atende às suposições da análise. Depois, o analista usa o modelo para predizer a rigidez.
A equação de regressão prediz que a rigidez de uma nova observação será 66,995 e que o intervalo de predição é [50, 85]. Apesar de ser improvável que a observação tenha uma rigidez de exatamente 66,995, o intervalo de predição indica que o engenheiro pode ter 95% de confiança de que o valor real estará entre 50 e 85.
O intervalo de predição é sempre mais amplo do que o intervalo de confiança correspondente porque prever uma única resposta é mais incerto do que prever a média de várias respostas.
