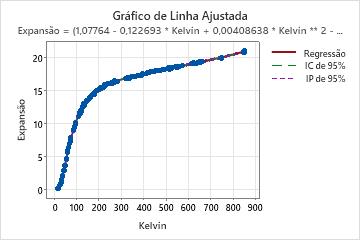
Gráfico de reta ajustada
Se seu modelo não linear contém apenas um preditor, o Minitab exibe o gráfico de linha ajustada para mostrar a relação entre os dados de resposta e do preditor. O gráfico inclui a linha de regressão, que representa a equação de regressão. Você também pode escolher exibir os intervalos de confiança de 95% e de predição no gráfico.
Interpretação
- A amostra contém um número adequado de observações ao longo de toda a faixa de todos os valores de predição.
- O modelo ajusta adequadamente qualquer curvatura aos dados. Para determinar qual modelo é melhor, examine o gráfico, o erro padrão da regressão (S) e o teste de ajuste (lack-of-fit) quando os seus dados contiverem repetições.
- Procure por todos os outliers, os quais podem exercer forte efeito sobre os resultados. Tente identificar a causa de qualquer outliers. Corrija os erros de entrada de dados ou de medição. Considere a remoção de valores de dados que estejam associados a eventos anormais que ocorrem somente uma vez (causas especiais). Em seguida, repita a análise. Para obter mais informações sobre detecção de outliers, vá para Observações atípicas.
Equação
Use a equação de regressão, para descrever a relação entre a resposta e os termos no modelo. A equação de regressão é uma representação algébrica da linha de regressão. Insira o valor de cada preditor na equação para calcular o valor médio de resposta. Ao contrário de regressão linear, de uma equação de regressão não linear pode ter muitas formas.
Para equações não lineares, determinar do efeito que cada preditor exerce sobre a resposta pode ser menos intuitivo do que para equações lineares. Ao contrário das estimativas dos parâmetros em modelos lineares, não há nenhuma interpretação consistente para as estimativas de parâmetros em modelos não lineares. A interpretação correta para cada parâmetro depende da função de expectativa e do lugar do parâmetro nele. Se seu modelo não-linear contém apenas um preditor, avalie o gráfico de linha ajustada para ver a relação entre o preditor e a resposta.
A convergência em uma solução não garante necessariamente que o modelo de ajuste é ideal ou que a soma dos quadrados dos erros (SSE) é minimizada. A convergência em valores de parâmetros incorretos pode ocorrer devido a um SSE local mínimo ou a uma função de expectativa incorreta. Portanto, é essencial examinar os valores dos parâmetros, gráfico de linha ajustada e gráficos de resíduos, para determinar se o modelo de ajuste de parâmetros e valores são razoáveis.
Interpretação
Nestes resultados, existe um preditor e sete estimativas de parâmetros. A variável de resposta é Expansão e a variável preditora é a temperatura na escala Kelvin. A equação longa descreve a relação entre a resposta e os preditores. O efeito que o aumento de 1 grau Kelvin tem sobre a expansão do cobre depende fortemente da temperatura inicial. O efeito das mudanças de temperatura sobre a expansão de cobre não pode ser facilmente resumido. Avalie o gráfico de linha ajustada para ver a relação entre o preditor e a resposta.
Se você inserir um valor para a temperatura em Kelvin na equação, o resultado é o valor ajustado para a expansão do cobre.
Equação
3) / (1 - 0,00576099 * Kelvin + 0,000240537 * Kelvin ** 2 - 1,23144E-07 * Kelvin ** 3)
IC de 95%
O intervalo de confiança do ajuste fornece um intervalo de valores prováveis para a resposta média dadas as configurações especificadas das preditoras.
Interpretação
Use o intervalo de confiança para avaliar a estimativa do valor ajustado para os valores observados das variáveis.
Por exemplo, com um nível de confiança de 95%, você pode ter 95% de confiança de que o intervalo de confiança contém a média da população para os valores especificados das variáveis no modelo. O intervalo de confiança ajuda a avaliar a significância prática de seus resultados. Use seu conhecimento especializado para determinar se o intervalo de confiança inclui valores que tenham significância prática para a sua situação. Um amplo intervalo de confiança indica que você pode estar menos confiante sobre a média de valores futuros. Se o intervalo for muito amplo para ser útil, pense em aumentar o tamanho da amostra.
PI de 95%
O intervalo de predição é um intervalo que provavelmente contém uma única resposta futura para um valor de variável da preditora dadas as configurações especificadas das preditoras.
Interpretação
Por exemplo, um engenheiro de materiais em uma fábrica de móveis desenvolve um modelo de regressão simples para predizer a rigidez de uma placa de aglomerado a partir da densidade da placa. O engenheiro verifica se o modelo atende às suposições da análise. Depois, o analista usa o modelo para predizer a rigidez.
A equação de regressão prediz que a rigidez de uma nova observação será 66,995 e que o intervalo de predição é [50, 85]. Apesar de ser improvável que a observação tenha uma rigidez de exatamente 66,995, o intervalo de predição indica que o engenheiro pode ter 95% de confiança de que o valor real estará entre 50 e 85.
O intervalo de predição é sempre mais amplo do que o intervalo de confiança correspondente porque prever uma única resposta é mais incerto do que prever a média de várias respostas.
