Neste tópico
Ajuste
Os valores ajustados também são chamados de ajustes ou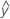 
. Os valores ajustados são estimativas de ponto da resposta do desvio padrão para dados valores dos preditores. Os valores dos preditores também são chamados de valores-x.
Interpretação
Valores ajustados são calculados inserindo os valores x específicos para cada observação no conjunto de dados para o modelo da equação.
Por exemplo, se a equação for ln (y) = ln (5 + 10x), o valor ajustado para o valor-x, 2, é 3,21888 (ln(5 + 10(2))).
As observações com valores ajustados que são muito diferentes do valor observado pode ser incomuns. As observações com valores de preditor incomuns podem ser influentes. Se o Minitab determinar que os dados incluem valores incomuns ou influentes, a saída inclui a tabela de tabela Ajustes e Diagnósticos para Observações Incomuns, que identifica essas observações. As observações com grandes resíduos padronizados não seguem bem a equação de regressão proposta. No entanto, espera-se que você tenha algumas observações incomuns. Por exemplo, com base nos critérios de grandes resíduos padronizados, espera-se que aproximadamente 5% das observações sejam sinalizadas como tendo um grande resíduo padronizados. Para obter mais informações sobre valores incomuns, acesse Observações atípicas.
Intervalo de confiança para a resposta original (IC de 95%)
Esses intervalos de confiança (IC) são faixas de valores que tendem a conter a resposta do desvio padrão da população que tem os valores observados dos preditores ou fatores no modelo.
Como as amostras são aleatórias, é improvável que duas amostras de uma população produzam intervalos de confiança idênticos. Mas, se você extrair amostras várias vezes, uma determinada porcentagem dos intervalos de confiança resultantes conterá o parâmetro populacional desconhecido. A porcentagem destes intervalos de confiança que contém o parâmetro é o nível de confiança do intervalo.
- Estimativa de ponto
- A estimativa de ponto é calculada a partir dos dados da amostra.
- Margem de erro
- A margem de erro define a largura do intervalo de confiança e é determinada pela variabilidade observada na amostra, o tamanho da amostra e o nível de confiança.
Interpretação
Use o intervalo de confiança para avaliar a estimativa do valor ajustado para os valores observados das variáveis.
Por exemplo, com um nível de confiança de 95%, é possível ter 95% de certeza de que o intervalo de confiança contém o desvio padrão do log da população para os valores especificados para as variáveis preditoras ou fatores no modelo. O intervalo de confiança ajuda a avaliar a significância prática de seus resultados. Use seu conhecimento especializado para determinar se o intervalo de confiança inclui valores que tenham significância prática para a sua situação. Um amplo intervalo de confiança indica que você pode estar menos confiante sobre o desvio padrão de valores futuros. Se o intervalo for muito amplo para ser útil, pense em aumentar o tamanho da amostra.
Razão dos resíduos
A razão dos resíduos é o desvio padrão observado dividido pelo valor ajustado.
Ln(Pad)
O log natural da resposta observada do desvio padrão.
Ln (Ajuste)
O log natural do desvio padrão ajustado.
EP Ln(Ajuste)
O erro padrão do logaritmo natural do desvio padrão ajustado estima a variação do desvio padrão calculado para as definições das variáveis especificadas. O cálculo do intervalo de confiança para a resposta média usa o erro padrão do ajuste. Os erros padrão são sempre não negativos.
Interpretação
Use o erro padrão do ajuste para medir a precisão da estimativa do log natural do desvio padrão. Quanto menor o erro padrão, mais precisa é a estimativa.
Intervalo de confiança para a resposta transformada (IC de 95%)
Esses intervalos de confiança (IC) são faixas de valores que tendem a conter o log natural do desvio padrão da população que tem os valores observados dos preditores ou fatores no modelo.
Como as amostras são aleatórias, é improvável que duas amostras de uma população produzam intervalos de confiança idênticos. Mas, se você extrair amostras várias vezes, uma determinada porcentagem dos intervalos de confiança resultantes conterá o parâmetro populacional desconhecido. A porcentagem destes intervalos de confiança que contém o parâmetro é o nível de confiança do intervalo.
- Estimativa de ponto
- A estimativa de ponto é calculada a partir dos dados da amostra.
- Margem de erro
- A margem de erro define a largura do intervalo de confiança e é determinada pela variabilidade observada na amostra, o tamanho da amostra e o nível de confiança.
Interpretação
Use o intervalo de confiança para avaliar a estimativa do valor ajustado para os valores observados das variáveis.
Por exemplo, com um nível de confiança de 95%, é possível ter 95% de certeza de que o intervalo de confiança contém o desvio padrão da população para os valores especificados para as variáveis preditoras ou fatores no modelo. O intervalo de confiança ajuda a avaliar a significância prática de seus resultados. Use seu conhecimento especializado para determinar se o intervalo de confiança inclui valores que tenham significância prática para a sua situação. Um amplo intervalo de confiança indica que você pode estar menos confiante sobre o desvio padrão de valores futuros. Se o intervalo for muito amplo para ser útil, pense em aumentar o tamanho da amostra.
Ln(Resíduos)
A diferença entre o logaritmo natural do desvio padrão da resposta observada e o logaritmo natural do desvio padrão ajustado. É o log do resíduo da razão.
Interpretação
O log dos resíduos representa a parte da resposta observada que não é explicada pelo modelo. Dos tipos de resíduos que o Minitab calcula em Análise de variabilidade, os log dos resíduos mais se assemelham a resíduos regulares.
Ln Pad (Resid)
Os resíduos padronizados para o log natural são iguais ao log dos resíduos dividido pelo seu erro padrão (assintótico)
Interpretação
Use os resíduos padronizados para o log natural a fim de ajudar a detectar outliers. Quando os valores de Ln Pad (Resid) estiverem entre −2 e 2, não existirão observações incomuns nos dados.
Resíduos padronizados maiores do que 2 e e menores do que -2 normalmente são considerados grandes. As observações que o Minitab rotula não seguem bem a equação de regressão proposta. No entanto, espera-se que você tenha algumas observações incomuns. Por exemplo, com base nos critérios de grandes resíduos padronizados, espera-se que aproximadamente 5% das observações sejam sinalizadas como tendo um grande resíduo padronizados. Para obter mais informações, vá para Observações atípicas.
Os resíduos padronizados são úteis porque resíduos brutos podem não ser bons indicadores de outliers. A variância de cada resíduo bruto pode diferir pelos valores-x associados a ela. Esta variação desigual faz com que seja difícil avaliar as magnitudes dos resíduos brutos. A padronização dos resíduos soluciona esse problema convertendo as diferentes variâncias a uma escala comum.
Hi (leverage)
Hi, também conhecido como leverage, mede a distância entre o valor x de uma observação e a média dos valores de x para todas as observações em um conjunto de dados.
Interpretação
Os valores de Hi ficam entre 0 e 1. O Minitab identifica as observações com valores de leverage maiores do que 3p/n ou 0,99, o que for menor, com um X na tabela Ajustes e Diagnósticos para Observações Incomuns . Em 3p/n, p é o número de coeficientes do modelo e o símbolo n representa o número de observações. As observações que os Minitab rotula com um 'X' podem ser influentes.
As observações influentes têm um efeito desproporcional sobre o modelo e podem produzir resultados enganosos. Por exemplo, a inclusão ou exclusão de um ponto influente pode mudar se um coeficiente for estatisticamente significativo ou não. As observações influentes podem ser pontos de leverage, outliers ou ambos.
Se você vir uma observação influente, determine se ela é um erro de entrada de dados ou de medição. Se a observação não não for nem um erro de entrada de dados nem um erro de medição, determine o quão influente uma observação é. Em primeiro lugar, ajustar o modelo com e sem a observação. Em seguida, compare os coeficientes, valores-p, R2, e outras informações do modelo. Se o modelo mudar significativamente quando você remover a observação influente, examine o modelo ainda mais para determinar se você especificou incorretamente o modelo. Talvez seja necessário reunir mais dados para resolver o problema.
Distância de Cook (D)
A distância de Cook (D) mede o efeito que tem uma observação sobre o conjunto de coeficientes em um modelo linear. A distância de Cook considera o valor de leverage e o resíduo padronizado de cada observação para determinar o efeito da observação.
Interpretação
As observações com um D alto podem ser consideradas influentes. Um critério habitualmente utilizado para um valor de D alto é quando D é maior do que a mediana da distribuição de F: F (0,5, p, n-p), onde p é o número de termos de modelos, incluindo a constante, e n é o número de observações. Outra maneira de examinar os valores de D é compará-los uns com os outros usando um gráfico, como um gráfico de valores individuais. As observações com valores de D alto em relação aos outros podem ser influentes.
As observações influentes têm um efeito desproporcional sobre o modelo e podem produzir resultados enganosos. Por exemplo, a inclusão ou exclusão de um ponto influente pode mudar se um coeficiente for estatisticamente significativo ou não. As observações influentes podem ser pontos de leverage, outliers ou ambos.
Se você vir uma observação influente, determine se ela é um erro de entrada de dados ou de medição. Se a observação não não for nem um erro de entrada de dados nem um erro de medição, determine o quão influente uma observação é. Em primeiro lugar, ajustar o modelo com e sem a observação. Em seguida, compare os coeficientes, valores-p, R2, e outras informações do modelo. Se o modelo mudar significativamente quando você remover a observação influente, examine o modelo ainda mais para determinar se você especificou incorretamente o modelo. Talvez seja necessário reunir mais dados para resolver o problema.
DFITS
DFITS mede o efeito que cada observação tem sobre os valores ajustados em um modelo linear. DFITS representa aproximadamente o número de desvios padrão que o valor ajustado muda quando cada observação é removida do conjunto de dados e o modelo é reajustado.
Interpretação
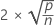
| Termo | Descrição |
|---|---|
| p | o número de termos no modelo |
| n | o número de observações |
Se você vir uma observação influente, determine se ela é um erro de entrada de dados ou de medição. Se a observação não não for nem um erro de entrada de dados nem um erro de medição, determine o quão influente uma observação é. Em primeiro lugar, ajustar o modelo com e sem a observação. Em seguida, compare os coeficientes, valores-p, R2, e outras informações do modelo. Se o modelo mudar significativamente quando você remover a observação influente, examine o modelo ainda mais para determinar se você especificou incorretamente o modelo. Talvez seja necessário reunir mais dados para resolver o problema.
