Neste tópico
Teste de múltiplas comparações
Intervalos de comparação múltiplos para amostras k > 2
Seja 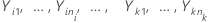 sejam k > 2 amostras independentes, cada amostra sendo independente e identicamente distribuída com a média
sejam k > 2 amostras independentes, cada amostra sendo independente e identicamente distribuída com a média 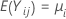 e variância
e variância  . E, suponhamos que as amostras sejam originárias a partir de populações que têm uma curtose comum.
. E, suponhamos que as amostras sejam originárias a partir de populações que têm uma curtose comum.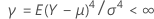
E seja 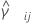 um estimador de curtose combinada para o par de amostras ( i, j) determinado como:
um estimador de curtose combinada para o par de amostras ( i, j) determinado como:
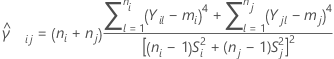
Seja 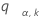 o ponto superior da faixa de variáveis de k que são independentes e identicamente distribuídas em uma distribuição aleatória normal. Ou seja,
o ponto superior da faixa de variáveis de k que são independentes e identicamente distribuídas em uma distribuição aleatória normal. Ou seja, 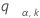 atende ao seguinte:
atende ao seguinte:
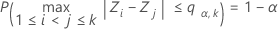
em que Z1, ..., Zk são variáveis aleatórias normais padrão independentes e identicamente distribuídas. Barnard (1978) fornece um algoritmo numérico simples com base em uma quadratura Gaussiana de 16 pontos para o cálculo da função de distribuição do intervalo normal.
O procedimento de múltiplas comparações rejeita a hipótese nula de igualdade de variâncias (também chamado de homogeneidade das variâncias) se, e somente se, pelo menos um par dos intervalos a seguir não se sobrepuserem:
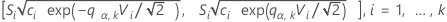
em que
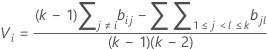
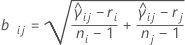
em que ri = (ni - 3) / ni .
Referimo-nos aos intervalos acima como intervalos de múltiplas comparações ou intervalos de MC. Os intervalos de MC para cada amostra não devem ser interpretados como intervalos de confiança para os desvios padrão das populações parentais. Hochbergetal. (1982) referem-se a intervalos semelhantes para comparar médias como "intervalos de incerteza". Os intervalos de MC apresentados aqui são úteis para a comparação de desvios padrão ou variâncias de experimentos de múltiplas amostras. Quando o teste de múltipla comparação global é significativo, os desvios padrão que correspondem aos intervalos não sobrepostos são estatisticamente diferentes. (Para a derivação detalhada destes intervalos, consulte o white paper sobre Métodos de múltiplas comparações.)
Intervalos de comparação múltiplos para amostras k = 2
Quando existem apenas duas amostras, os intervalos de múltipla comparação são dados por:

em que zα / 2 é o ponto do percentil α / 2 superior da distribuição da normal padrão, ci = ni / ni - zα / 2 e Vi é dado pela seguinte fórmula:
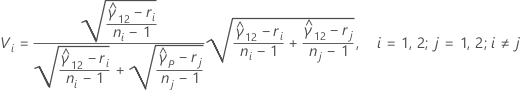
Valor de P parar teste
Se houver 2 amostras no experimento, o Minitab calcula o valor de p para o teste de múltiplas comparações pelo método de Bonetti para um teste de 2 variâncias e uma proporção hipotética, Ρo , de 1.
Se houver k > 2 amostras no experimento, então, seja Pi j o valor de p do teste para qualquer par (i, j ) de amostras. O valor de p para o procedimento de múltiplas comparações como um teste geral de igualdade de variâncias é dado da seguinte maneira:

Para obter mais informações, incluindo simulações e algoritmos detalhados para calcular Pi j , acesse Método de Bonett, que é um white paper que tem simulações e outras informações sobre o método de Bonett.
Notação
| Termo | Descrição |
|---|---|
| ni | número de observações na amostra i |
| Y i l | a Ia observação na amostra i |
| mi | a média aparada para a amostra i com a proporção de corte de  |
| k | o número de amostras. |
| Si | o desvio padrão da amostra i |
| α | o nível de significância para o teste = 1 - (o nível de confiança / 100) |
| Ci | 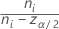 |
| Zα / 2 | o ponto percentil superior α/2 da distribuição normal padrão |
| ri |  |
Estatística de teste e Levene
O Minitab apresenta uma estatística de teste e um valor de p para o teste de Levene. A hipótese nula é que as variâncias são iguais, e a hipótese alternativa é que as variâncias não são iguais. Use o teste de Levene quando os dados forem provenientes de distribuições contínuas, mas não necessariamente normais.
O método de cálculo para o teste de Levene é uma modificação do procedimento de Levene (Levene, 1960) que foi desenvolvido por Brown e Forsythe (1974). Esse método considera as distâncias das observações da mediana da amostra em vez da média da amostra. O uso da mediana da amostra, em vez da média da amostra, torna o teste mais robusto para amostras de menor dimensão e torna o procedimento assintoticamente livre de distribuição. Se o valor de p for menor do que o de seu nível de α, rejeite a hipótese nula de que as variâncias são iguais.
Fórmula
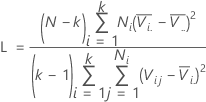
- H. Levene (1960). Contributions to Probability and Statistics. Stanford University Press, CA.
- M. B. Brown e A. B. Forsythe (1974). "Robust tests for the equality of variance," Journal of the American Statistical Association, 69, 364-367.
Notação
| Termo | Descrição |
|---|---|
| Vij |  |
| i | 1, ..., k |
| j | 1, ..., ni |
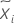 | mediana |
Estatística de teste de Bartlett
O Minitab apresenta uma estatística de teste e um valor de p para o teste de Bartlett. Quando existem apenas dois níveis, o Minitab executa o teste F em vez do teste de Bartlett. Para estes testes, a hipótese nula é que as variâncias são iguais, e a hipótese alternativa é que os desvios não são iguais. Use o teste de Bartlett quando os dados forem provenientes de distribuições normais; o teste de Bartlett não é robusto para desvios da normalidade.
A estatística de teste de Bartlett calcula a média aritmética ponderada e a média geométrica ponderada de cada variância da amostra com base nos graus de liberdade. Quanto maior a diferença nas médias, maior é a probabilidade de variâncias das amostras não serem iguais. B segue uma distribuição χ2 com k – 1 graus de liberdade. Se o valor de p for menor do que o de seu nível de α, rejeite a hipótese nula de que as variâncias são iguais.
Fórmula
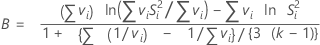
Notação
| Termo | Descrição |
|---|---|
| Si |  |
| k | número de amostras |
| vi | ni - 1 |
| ni | número de observações no io nível de fator |
Estatística do teste F
Quando existem apenas dois níveis, o Minitab executa o teste F em vez do teste de Bartlett. A hipótese nula é que as variâncias são iguais, e a hipótese alternativa é que as variâncias não são iguais. Use a estatística F, quando os dados são de distribuições normais.
Se o valor de p for menor que o nível de α, rejeite a hipótese nula de que as variâncias são iguais.
Fórmula
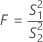
Fórmula para o valor de p
- Para um teste unilateral com uma hipótese alternativa de "menor que", o valor de p é igual à probabilidade de se obter uma estatística F que seja igual ou menor do que o valor observado a partir de uma distribuição-F com graus de liberdade DF1 e DF2.
- Para um teste bilateral em que a razão é menor que 1, o valor de p é igual a duas vezes a área sob a curva F menor que o valor observado a partir de uma distribuição F com graus de liberdade DF1 e DF2.
- Para um teste bilateral em que a razão é maior que 1, o valor de p é igual a duas vezes a área sob a curva F maior que o valor observado a partir de uma distribuição F com graus de liberdade DF1 e DF2.
- Para um teste unilateral com uma hipótese alternativa de "maior que", o valor de p é igual à probabilidade de se obter uma estatística F que seja igual ou maior do que o valor observado a partir de uma distribuição-F com graus de liberdade DF1 e DF2.
Notação
| Termo | Descrição |
|---|---|
| S12 | variância da amostra 1 |
| S22 | variância da amostra 2 |
| n1 - 1 | graus de liberdade do numerador |
| n2 - 1 | graus de liberdade do denominador |
Desvio padrão (StDev)
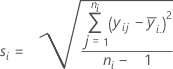
Notação
| Termo | Descrição |
|---|---|
| yij | observações no io nível de fator |
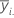 | média de observações no io nível de fator |
| ni | número de observações no io nível de fator |
Intervalos de confiança de Bonferroni
O Minitab calcula intervalos de confiança para os desvios padrão usando o método de Bonferroni. Um intervalo de confiança é uma faixa de valores que tende a incluir algum parâmetro da população, neste caso, contêm o desvio padrão.
Os intervalos de confiança padrão são calculados utilizando-se um nível de confiança de 1 - α / 2. O método de Bonferroni utiliza o nível de confiança de 1 - α / 2p para cada intervalo de confiança individual, em que p é o número de combinações de fatores e de nível. O método garante que o conjunto de intervalos de confiança tem um nível de confiança de pelo menos 1 - α. O método de Bonferroni fornece intervalos de confiança mais conservadores (mais amplos), o que reduz a probabilidade de um erro tipo 1.
