Neste tópico
- Análises disponíveis para dados não normais
- Usar Análise Automatizada de Capacidade para selecionar um método
- Exemplo de uso Análise Automatizada de Capacidade para selecionar um método
- Use Identificação de distribuição individual para encontrar uma distribuição ou transformação apropriada
- Exemplo de uso de Identificação de distribuição individual para comparar acessos de distribuições e transformações
Análises disponíveis para dados não normais
- Selecione um modelo de distribuição não normal que ajusta seus dados e, em seguida, analisar os dados usando uma análise de capacidade para dados não normais, como Análise de capacidade não normal.
- Transforme os dados para que a distribuição normal seja um modelo apropriado, e use uma análise de capacidade para dados normais, como Análise de capacidade normal.
- Selecione um método não paramétrico que não faça suposições sobre a distribuição dos dados, como Análise de Capacidade (Não Paramétrica).
- Use o conhecimento de engenharia ou o histórico do seu processo.
- Muito frequentemente, é melhor usar o conhecimento de engenharia e o histórico do seu processo para identificar uma método que se ajusta aos dados do seu processo. Por exemplo, os dados seguem uma distribuição simétrica? Que método funcionou no passado para situações semelhantes?
- Use avaliações de qualidade de ajuste.
- O teste de Anderson-Darling avalia se uma determinada distribuição se ajusta aos dados de um processo. Os gráficos de probabilidade são outra ferramenta que avalia o quanto os dados seguem uma distribuição.
- Avalie como diferentes métodos afetam suas conclusões.
- Se vários métodos fornecem um ajuste adequado aos dados e conclusões semelhantes, então a escolha é menos consequente. Por outro lado, se suas conclusões dependem do método, você pode querer relatar a conclusão mais conservadora ou coletar mais informações. Por exemplo, você pode usar os resultados da distribuição de Análise Automatizada de Capacidade ou os percentis de Identificação de distribuição individual para ver como suas conclusões dependem do método.
- Se você planeja executar repetidas análises de capacidade em seu processo ao longo do tempo, tente usar um método que provavelmente caracterize adequadamente seu processo consistentemente ao longo do tempo. O uso do mesmo método permite comparar fácil e diretamente os índices das análises repetidas.
- Os modelos não normais e não paramétricos usam as unidades de dados reais. O modelo normal de uma transformação usa unidades transformadas.
- O modelo normal de uma transformação fornece estimativas da capacidade geral e dentro do processo.
Use Análise Automatizada de Capacidade para que o Minitab Statistical Software ajude a determinar um método razoável que se ajuste aos dados, considerando a utilidade e a praticidade do método. A análise considera primeiro distribuições e depois transformações. Se nenhum modelo se ajustar aos dados, a análise usará o método não paramétrico.
Para ver mais detalhes sobre os dados, use Identificação de distribuição individual. A análise fornece medidas de qualidade de ajuste para diferentes métodos para apoiar sua decisão sobre qual método usar.
Usar Análise Automatizada de Capacidade para selecionar um método
Use Análise Automatizada de Capacidade para avaliar a compatibilidade de vários métodos com os dados e fazer uma seleção razoável.
- Escolha .
- Especifique se seus dados estão organizados em uma única coluna ou entre linhas.
- Insira os limites de especificação para o processo.
A análise considera distribuições e, em seguida, transformações. Se nenhum método paramétrico se ajustar aos dados, a análise usará o método não paramétrico. Os resultados incluem um relatório de capacidade para o primeiro método que fornece um ajuste razoável. A tabela de resultados da distribuição mostra a ordem da avaliação dos métodos, informações sobre o ajuste dos métodos e estatísticas de capacidade. Você pode produzir resultados para um método alternativo para investigar os métodos em mais detalhes.
Exemplo de uso Análise Automatizada de Capacidade para selecionar um método
Um engenheiro coleta dados sobre a extensão do empenamento em revestimentos cerâmicos. A distribuição dos dados é desconhecida, então ela executa Identificação de distribuição individual os dados para determinar um método razoável para uma análise de capacidade.
A tabela de distribuição dos resultados mostra a ordem de avaliação dos métodos. Na primeira linha, a conclusão para o teste de Anderson-Darling é que os dados não seguem uma distribuição normal ao nível de significância de 0,05, pois o valor de p é menor que 0,05. Na segunda linha, a conclusão para o teste de Anderson-Darling é que a distribuição de Weibull é um ajuste razoável aos dados, pois o valor de p é maior que 0,05. Os resultados de capacidade são para a distribuição Weibull porque a distribuição Weibull é o primeiro método na lista que fornece um ajuste razoável.
Os engenheiros usam o conhecimento do processo para considerar se a distribuição Weibull é um método razoável. Por exemplo, a distribuição Weibull tem um limite em 0. Nos dados, 0 é um limite que representa um bloco não distorcido.
A análise inclui uma análise de capacidade que usa a distribuição Weibull.
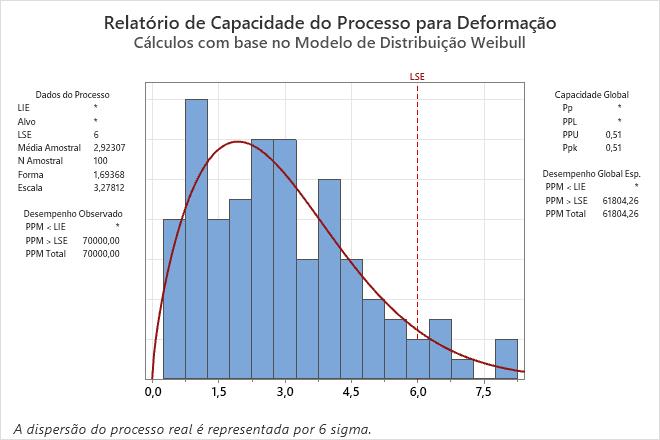
Resultados da distribuição automatizada de capacidades: Deformação
| Distribuição | Local | Escala | Limite | Forma | P | Ppk | Cpk |
|---|---|---|---|---|---|---|---|
| Normal | 2,9231 | 1,7860 | 0,0100421 | 0,5743 | 0,5838 | ||
| Weibull* | 3,2781 | 1,6937 | >0,25 | 0,5133 | |||
| Lognormal | 0,8443 | 0,7444 | <0,005 | 0,4242 | |||
| Menor Valor Extremo | 3,8641 | 1,9924 | <0,01 | 0,5362 | |||
| Maior Valor Extremo | 2,0958 | 1,4196 | 0,212835 | 0,5130 | |||
| Gama | 1,2477 | 2,3428 | 0,238337 | 0,4851 | |||
| Logística | 2,7959 | 1,0162 | 0,0127347 | 0,5799 | |||
| Loglogística | 0,9097 | 0,4217 | <0,005 | 0,4090 | |||
| Exponencial | 2,9231 | <0,0025 | 0,3780 | ||||
| Weibull de 3 Parâmetros | 2,9969 | 0,2099 | 1,5049 | 0,467097 | 0,4980 | ||
| Lognormal de 3 Parâmetros | 1,3788 | 0,4184 | -1,4002 | 0,4961 | |||
| Gama de 3 Parâmetros | 1,2314 | -0,0197 | 2,3898 | 0,4864 | |||
| Loglogística de 3 Parâmetros | 1,3043 | 0,2700 | -1,0940 | 0,4656 | |||
| Exponencial de 2 Parâmetros | 2,6679 | 0,2552 | <0,01 | 0,3982 | |||
| Transformação de Box-Cox | 1,6237 | 0,5380 | 0,574337 | 0,5116 | 0,5214 | ||
| Transformação de Johnson | 0,0112 | 0,9949 | 0,798895 | 0,4959 | |||
| Não-paramétrico | 0,6187 |
Use Identificação de distribuição individual para encontrar uma distribuição ou transformação apropriada
Use Identificação de distribuição individual antes de realizar uma análise de capacidade para determinar qual distribuição ou transformação é a mais apropriada para seus dados. Se nenhuma distribuição ou transformação for compatível com seus dados, considere o Análise de Capacidade (Não Paramétrica).
- Escolha .
- Selecione se seus dados são organizados em uma única coluna ou entre linhas.
- Escolha Usar todas as distribuições e transformações ou Especificar e escolha até 4 distribuições e transformações para testar.
- Análise de capacidade não normal
- Análise de capacidade não normal para múltiplas variáveis
- Capability Sixpack não normal
- Análise de capacidade normal
- Capability Sixpack normal
- Análise de capacidade normal para múltiplas variáveis
- Análise de capacidade entre/dentro
Exemplo de uso de Identificação de distribuição individual para comparar acessos de distribuições e transformações
Um engenheiro coleta dados sobre a extensão do empenamento em revestimentos cerâmicos. A distribuição dos dados é desconhecida, portanto, ela realiza Identificação de distribuição individual nos dados para comparar qualidade do ajuste entre a distribuição exponencial e a distribuição normal após uma transformação de Johnson.
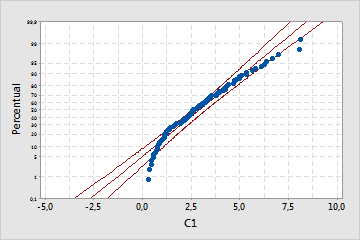
Distribuição exponencial
Este gráfico de probabilidades indica que a distribuição exponencial não é um bom ajuste; o valor-p é baixo o bastante para rejeitar a hipótese nula de que os dados seguem uma distribuição exponencial.
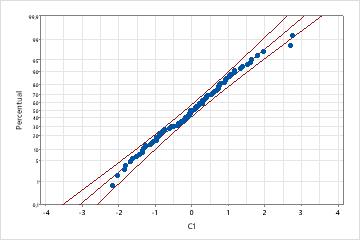
Distribuição normal com a transformação de Johnson
Contudo, depois de aplicar uma transformação de Johnson, os dados seguem de perto uma distribuição normal porque o valor-p é grande, e quase todos os pontos de dados se encaixam dentro dos limites de confiança do gráfico de probabilidade normal.
