N
O tamanho da amostra (N) é o número total de observações na amostra original. O Minitab usa reamostras deste tamanho de amostra para formar amostras de bootstrap.
Média
A média é a média dos dados, que é a soma de todas as observações divididas pelo número de observações.
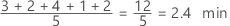
Interpretação
Use a média para descrever a amostra com um único valor que representa o centro dos dados. Diversas análises estatísticas usam a média como uma média padrão do centro da distribuição dos dados.
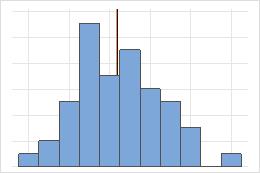
Simétrica
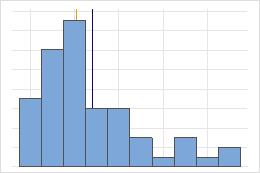
Não simétrica
Para a distribuição simétrica, a média (linha azul) e a mediana (linha laranja) são tão similares que você não pode ver facilmente as linhas. Mas a distribuição não simétrica é assimétrica à direita.
StDev
O desvio padrão é a medida mais comum de dispersão, ou o quanto os dados estão dispersos sobre a média. O símbolo σ (sigma) é frequentemente usado para representar o desvio padrão de uma população, enquanto s é usado para representar o desvio padrão de uma amostra. A variação que é aleatória ou natural de um processo é frequentemente referida como ruído.
Como o desvio padrão está nas mesmas unidades que os dados, ele é normalmente mais fácil de interpretar do que a variância.
Interpretação
Use o desvio padrão para determinar o grau de dispersão dos dados a partir da média. Um valor de desvio padrão mais alto indica maior dispersão nos dados. Uma boa regra de ouro de uma distribuição normal é que aproximadamente 68% dos valores estão dentro de um desvio padrão da média, 95% dos valores estão dentro de dois desvios padrão e 99,7% dos valores estão dentro de três desvios padrão.
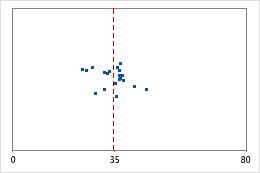
Hospital 1
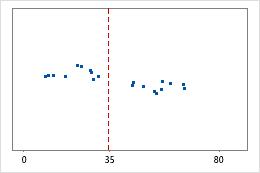
Hospital 2
Tempos de alta de hospital
Os administradores controlam o tempo gasto na alta de pacientes tratados nos departamentos de emergência de dois hospitais. Apesar de os tempos médios de alta serem quase os mesmos (35 minutos), os desvios padrão são significativamente diferentes. O desvio padrão do hospital 1 é de cerca de 6. Em média, o tempo de alta de um paciente se desvia da média (linha tracejada) em cerca de 6 minutos. O desvio padrão do hospital 2 é de cerca de 20. Na média, um tempo de alta de um paciente se desvia da média (linha tracejada) em cerca de 20 minutos.
Variância
A variância mede o quanto os dados estão dispersos em relação à sua média. A variância é igual ao desvio padrão ao quadrado.
Interpretação
Quanto maior a variância, maior a dispersão nos dados.
Como a variância (σ2) é uma quantidade quadrada, suas unidades também são quadradas, o que torna a variância difícil de usar, na prática. O desvio padrão é normalmente mais fácil de interpretar porque ele está nas mesmas unidades que os dados. Por exemplo, uma amostra de tempos de espera em uma parada de ônibus pode ter uma média de 9 minutos2. Como a variância não está nas mesmas unidades que os dados, com frequência, ela é exibida com sua raiz quadrada, o desvio padrão. Uma variância de 9 minutos2 é equivalente a um desvio padrão de 3 minutos.
Mínimo
O mínimo é o menor valor de dados.
Em nesses dados, o mínimo é 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretação
Use o mínimo para identificar um possível outlier ou um erro de entrada de dados. Uma das maneiras mais simples para avaliar a dispersão de seus dados é comparar o mínimo e o máximo. Se o valor mínimo for muito baixo, mesmo quando se considerar o centro, a dispersão e o formato dos dados, investigue a causa do valor extremo.
Mediana
A mediana é o ponto médio do conjunto de dados. Este valor do ponto médio é o ponto em que metade das observações estão acima do valor e metade das observações estão abaixo do valor. A mediana é determinada por classificar as observações e encontrar a observação que está no número [N + 1] / 2 na ordem de grandeza. Se o número de observações for ímpar, a mediana é o valor médio das observações que são classificadas com números de N / 2 e [N / 2] + 1.
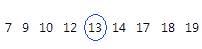
Para esses dados ordenados, a mediana é 13. Isto é, metade dos valores é menor ou igual a 13, e metade dos valores é maior ou igual a 13. Se você adicionar outra observação igual a 20, a mediana será 13,5, que é a média entre a 5a observação (13) e a 6a observação (14).
Interpretação

Simétrica

Não simétrica
Para a distribuição simétrica, a média (linha azul) e a mediana (linha laranja) são tão similares que você não pode ver facilmente as linhas. Mas a distribuição não simétrica é assimétrica à direita.
Máximo
O valor máximo é o maior valor de dados.
Nesses dados, o máximo é 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretação
Use o máximo para identificar um possível outlier ou um erro de entrada de dados. Uma das maneiras mais simples para avaliar a dispersão de seus dados é comparar o mínimo e o máximo. Se o valor máximo for muito elevado, mesmo quando se considerar o centro, a dispersão e o formato dos dados, investigue a causa do valor extremo.
Diferença em Médias Observadas
O Minitab indica qual média de população é subtraída da outra. A diferença é a diferença entre as médias das duas amostras. Esta diferença nos meios observados é uma estimativa da diferença nas médias populacionais. Para estimar um intervalo de confiança para a diferença nas médias de dois grupos independentes, use Bootstrap para média de duas amostras.
