Neste tópico
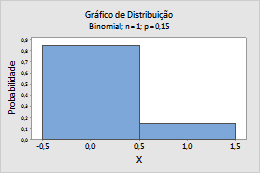
Bernoulli
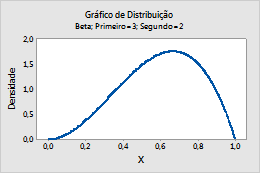
Beta
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição Beta.
- Em Primeiro parâmetro de forma, insira um número que seja maior do que zero para o primeiro parâmetro de forma.
- Em Segundo parâmetro de forma, insira um número que seja maior do que zero para o segundo parâmetro de forma.
Por exemplo, este gráfico mostra uma distribuição beta que tem uma primeira forma de 3 e uma segunda forma de 2.
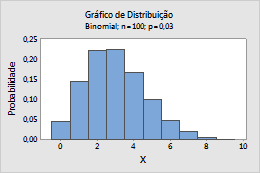
Binomial
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição binomial.
- Em Número de ensaios, insira o tamanho amostral.
- Em Probabilidade do evento, insira um número entre 0 e 1, para a probabilidade de que ocorra o resultado de interesse. Uma ocorrência é chamada um "evento".
Por exemplo, este gráfico mostra uma distribuição binomial que tem 100 ensaios e uma probabilidade eventos de 0,03.
Cauchy
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição Cauchy.
- Em Local, insira um valor que representa a localização do pico da distribuição.
- Em Escala, insira um valor que representa a dispersão da distribuição.
Por exemplo, este gráfico mostra uma distribuição Cauchy que tem uma localização de 0, numa escala de 1.
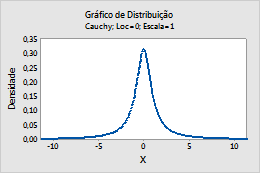
Qui-quadrado
Em Graus de liberdade, insira o número de graus de liberdade que definem o Distribuição Qui-Quadrado.
Por exemplo, este gráfico mostra uma distribuição qui-quadrado que tem 4 graus de liberdade.
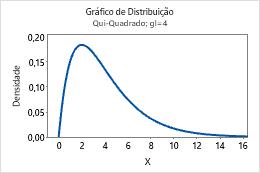
Discreta
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição discreta.
- Em Valores em, insira a coluna que contém os valores a serem incluídos na distribuição. Normalmente, os valores são eventos discretos ou contagens que são representados por valores numéricos.
- Em Probabilidades em, insira a coluna que contém as probabilidades para cada valor. As probabilidades deve estar entre 0 e 1, e devem somar 1.
Nesta worksheet, Valor contém as contagens a serem incluídas na distribuição e Probabilidade contém a probabilidade de cada contagem.
| C1 | C2 |
|---|---|
| Valor | Probabilidade |
| 0 | 0,03 |
| 1 | 0,13 |
| 2 | 0,70 |
| 3 | 0,10 |
| 4 | 0,04 |
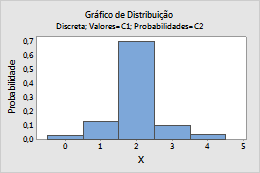
Exponencial
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição exponencial.
- Em Escala, insira o parâmetro de escala. O parâmetro de escala é igual à média quando o parâmetro de limite for igual a 0.
- Em Limite, insira o limite inferior da distribuição.
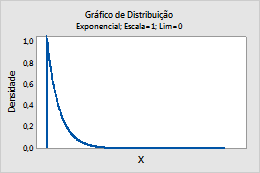
Por exemplo, este gráfico mostra uma distribuição exponencial que possui uma escala de 1 e um limite de 0.
F
Em Graus de liberdade do numerador e Graus de liberdade do denominador, insira o numerador e os graus de liberdade do denominador para definir a distribuição F.Para obter mais informações, vá para Distribuição F.
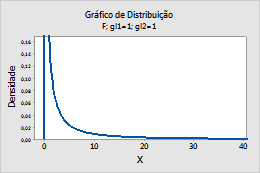
Por exemplo, este gráfico mostra uma distribuição F que tem 1 grau de liberdade de numerador e 1 grau de liberdade de denominador.
Gama
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição gama.
- Em Parâmetro de forma, insira um valor que representa a forma da distribuição.
- Em Parâmetro da escala, insira um valor que representa a escala da distribuição.
- Em Parâmetro de limite, insira o limite inferior da distribuição.
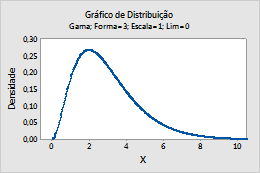
Por exemplo, este gráfico mostra uma distribuição gama que tem uma forma de 3, uma escala de 1 e um limite de 0.
Geométrica
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição geométrica.
- Em Probabilidade do evento, insira um número entre 0 e 1 para a probabilidade de ocorrência de cada tentativa. Uma ocorrência é chamada um "evento".
- Para especificar qual a versão da distribuição geométrica deve ser usada, clique em Opções, e escolha uma das seguintes opções:
- Modelar o número total de ensaios: Modelar o número total de tentativas que são necessárias para produzir um evento.
- Modelar apenas o número de não-eventos: Modelar o número de não-eventos que ocorrem antes que ocorra um evento.
Dica
Para mudar as configurações padrão para futuras sessões do Minitab, selecione .
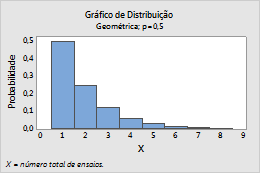
Por exemplo, este gráfico mostra uma distribuição geométrica que modela o número total de ensaios, e tem uma probabilidade eventos de 0,5.
Hipergeométrica
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição Hipergeométrica.
- Em Tamanho da população (N), insira o número total de itens na população (N). Quando N for muito grande para ser conhecido, a distribuição binomial se aproxima da distribuição hipergeométrica.
- Em Contagem de eventos na população (M), insira um número entre 0 e N (tamanho da população) para representar o número de eventos na população.
- Em Tamanho amostral (n), insira o número de itens que são amostrados sem substituição.
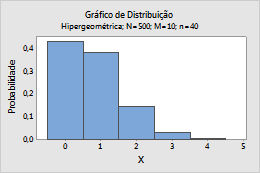
Por exemplo, esta figura mostra uma distribuição hipergeométrica que tem uma população de 400, uma contagem de evento de 10 e um tamanho amostral de 40.
Inteira
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição inteira.
- Em Valor mínimo, insira a extremidade inferior da distribuição.
- Em Valor máximo, insira a extremidade superior da distribuição.
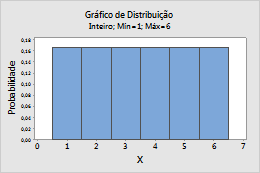
Por exemplo, este gráfico mostra uma distribuição inteira que tem um valor mínimo de 1 um valor máximo de 6.
Laplace
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição de Laplace.
- Em Local, insira um valor que representa a localização do pico da distribuição.
- Em Escala, insira um valor que representa a dispersão da distribuição.
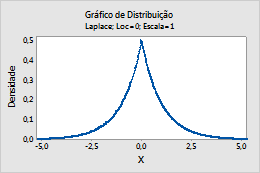
Por exemplo, este gráfico mostra uma distribuição Laplace que tem uma localização de 0, numa escala de 1.
Maior valor extremo
Conclua as etapas a seguir para inserir os parâmetros para a distribuição de maior valor extremo. Para obter mais informações, acesse Distribuições do menor e maior valores extremos.
- Em Local, insira um valor que representa a localização do pico da distribuição.
- Em Escala, insira um valor que representa a dispersão da distribuição.
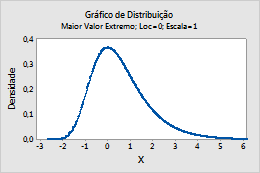
Por exemplo, este gráfico mostra uma distribuição de maior valor extremo que tem uma localização de 0 e uma escala de 1.
Logística
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição logística.
- Em Local, insira um valor que representa a localização do pico da distribuição.
- Em Escala, insira um valor que representa a dispersão da distribuição.
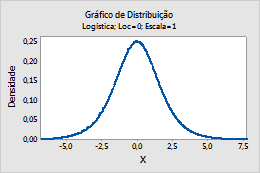
Por exemplo, este gráfico mostra uma distribuição logística que tem uma localização de 0, numa escala de 1.
Loglogística
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição loglogística.
- Em Local, insira um valor que representa a localização do pico da distribuição logística relacionada.
- Em Escala, insira um valor que representa a dispersão da distribuição logística relacionada.
- Em Limite, insira o limite inferior da distribuição.
Por exemplo, este gráfico mostra uma distribuição loglogística que tem uma localização de 0, numa escala de 1 e um limite de 0.
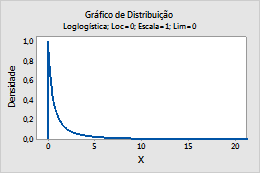
Lognormal
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição lognormal.
- Em Local, insira um valor que representa a localização do pico da distribuição normal relacionada.
- Em Escala, insira um valor que representa a dispersão da distribuição normal relacionada.
- Em Limite, insira o limite inferior da distribuição.
Por exemplo, este gráfico mostra uma distribuição lognormal que tem uma localização de 0, numa escala de 1 e um limite de 0.
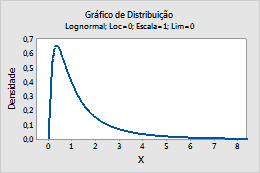
Normal multivariado
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição Normal Multivariada.
- Em Coluna de média, insira a coluna que contém o vetor de médias.
- Em Matriz de variância-covariância, insira a matriz (por exemplo, M1) que contém as variâncias e covariâncias das variáveis na mesma ordem que na coluna de média.
Neste exemplo, os dados são de três variáveis aleatórias normais e correlacionadas. As médias estão em C1 e a matriz de variância-covariância é nas colunas C2-C4.
| C1 | C2 | C3 | C4 |
|---|---|---|---|
| 2,0 | 13,0321 | 2,6544 | 0,0899 |
| 100,1 | 2,6544 | 6,5883 | 1,4438 |
| 151,3 | 0,0899 | 1,4438 | 12,2219 |
- Selecione .
- Em Copiar de colunas, insira C2-C4.
- Em Armazenamento de Dados Copiados, sob Na worksheet atual, na matriz:, insira M1.
- Clique em OK.
Agora, você pode gerar dados aleatórios a partir da distribuição normal multivariada.
- Selecione .
- Em Número de linhas de dados a serem geradas, digite o número de linhas que você deseja. Para este exemplo, digite 18.
- Em Armazenar em coluna(s), insira as colunas de armazenamento. Para este exemplo, insira C6-C8.
- Em Coluna de média, insira a coluna que contém as médias. Para este exemplo, insira C1.
- Em Matriz de variância-covariância, insira a matriz. Para este exemplo, insira M1.
- Clique em OK.
Dica
Para obter a mesma amostra que na tabela abaixo, defina a base de gerador aleatório antes de gerar a amostra aleatória. Escolha e insira 5.
| C6 | C7 | C8 |
|---|---|---|
| 1,61033 | 99,192 | 148,814 |
| 0,45883 | 96,093 | 144,679 |
| −0,46745 | 101,041 | 148,936 |
| … | … | … |
Binomial negativa
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição binomial negativa.
- Em Probabilidade do evento, insira um número entre 0 e 1 para a probabilidade de ocorrência de cada tentativa. Uma ocorrência é chamada um "evento".
- Em Número de eventos necessários, insira um número inteiro positivo, que represente o número de vezes que o evento deve ocorrer.
- Para especificar qual a versão da distribuição binomial negativa deve ser usada, clique em Opções, e escolha uma das seguintes opções:
- Modelar o número total de ensaios: Modelar o número total de tentativas que são necessárias para produzir o número especificado de eventos.
- Modelar apenas o número de não-eventosModelar o número de não-eventos que ocorrem antes ocorrerem o número de eventos.
Dica
Para mudar as configurações padrão para futuras sessões do Minitab, selecione .
Por exemplo, este gráfico mostra uma distribuição binomial negativa que modela o número total de ensaios, e tem uma probabilidade eventos de 0,5 e 5 eventos.
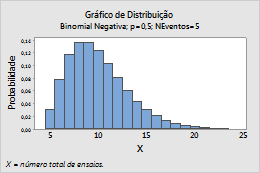
Normal
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição normal.
- Em Média, insira o valor para o centro da distribuição.
- Em Desvio padrão, insira o valor para a dispersão da distribuição.
Por exemplo, este gráfico mostra uma distribuição normal que tem uma média de 0 e um desvio padrão de 1.
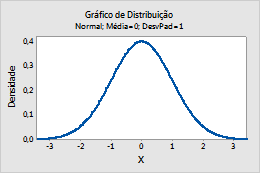
Poisson
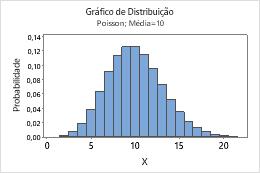
Em Média, insira o valor para a taxa média de ocorrência.Para obter mais informações, vá para Distribuição de Poisson.
Por exemplo, este gráfico mostra uma distribuição de Poisson que tem uma média de 10.
Menor valor extremo
Conclua as etapas a seguir para inserir os parâmetros para a distribuição de menor valor extremo. Para obter mais informações, acesse Distribuições do menor e maior valores extremos.
- Em Local, insira um valor que representa a localização do pico da distribuição.
- Em Escala, insira um valor que representa a dispersão da distribuição.
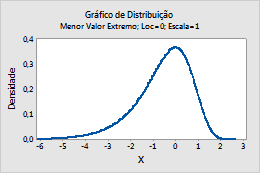
Por exemplo, este gráfico mostra uma distribuição de menor valor extremo que tem uma localização de 0 e uma escala de 1.
t
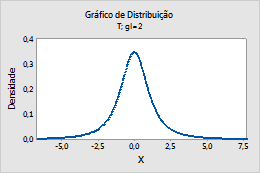
Em Graus de liberdade, insira os graus de liberdade para definir a distribuição t.Para obter mais informações, vá para Distribuição-t.
Por exemplo, este gráfico mostra uma distribuição t que tem 2 graus de liberdade.
Triangular
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição triangular.
- Em Ponto extremo inferior, insira o valor mínimo para a distribuição.
- Em Moda, insira o valor para o pico da distribuição.
- Em Ponto extremo superior, insira o valor máximo para a distribuição.
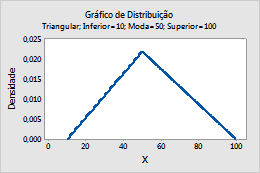
Por exemplo, esta figura mostra uma distribuição triangular que tem um ponto de extremidade inferior de 10, um modo de 50 e um ponto de extremidade superior de 100.
Uniforme
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição uniforme.
- Em Ponto extremo inferior, insira o valor mínimo para a distribuição.
- Em Ponto extremo superior, insira o valor máximo para a distribuição.
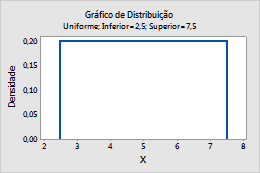
Por exemplo, este gráfico mostra uma distribuição uniforme, que tem um ponto de extremidade inferior de 2,5 e um ponto de extremidade superior de 7,5.
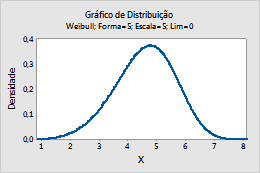
Weibull
Conclua as etapas a seguir para inserir os parâmetros para o Distribuição Weibull.
- Em Parâmetro de forma, insira um valor que representa a forma da distribuição.
- Em Parâmetro da escala, insira um valor que representa a escala da distribuição.
- Em Parâmetro de limite, insira o limite inferior da distribuição.
Por exemplo, este gráfico mostra uma distribuição Weibull que tem uma localização de 5, numa escala de 5 e um limite de 0.