A materials engineer for a building products manufacturer is developing a new insulation product. The engineer designs a 2-level full factorial experiment to assess several factors that could impact the strength, density, and insulating value of the insulation.
The engineer analyzes a factorial design to determine how material type, injection pressure, injection temperature, and cooling temperature affect the strength of the insulation.
- Open the sample data, InsulationProperties.MWX.
- Choose .
- In Responses, enter Strength.
- Click Terms.
- Under Include terms in the model up through order, choose 2.
- Click OK and then click Covariates.
- In Covariates, enter MeasTemp.
- Click OK and then click Graphs.
- Under Residual Plots, select Four in one.
- Click OK in each dialog box.
Interpret the results
In the Analysis of Variance table, the p-values for all the linear terms—Material, InjPress, InjTemp, and CoolTemp—are significant. Because the p-values are less than the significance level of 0.05, the engineer concludes that the effects are statistically significant. The covariate MeasTemp is not significant (P-Value = 0.278). None of the two-way interactions are significant. The engineer can consider reducing the model.
The R2 value shows that the model explains 98.02% of the variance in strength, which indicates that the model fits the data extremely well.
Most of the VIFs are small, which indicates that the terms in the model are not correlated. The VIF for MeasTemp is 5.87, but this term is not significant, and you would not include it in the final model.
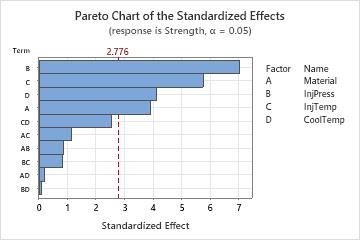
The Pareto plot of the effects allow you to visually identify the important effects and compare the relative magnitude of the various effects. In addition, you can see that the largest effect is injection pressure (B) because it extends the farthest. The effect for the injection pressure by cooling temperature interaction (BD) is the smallest because it extends the least.
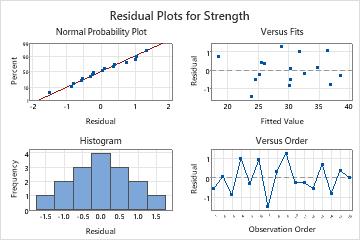
The residual plots do not indicate any problems with the model.
Coded Coefficients
| Term | Effect | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|---|
| Constant | 56.0 | 21.0 | 2.66 | 0.056 | ||
| MeasTemp | -1.229 | 0.979 | -1.25 | 0.278 | 5.87 | |
| Material | 5.316 | 2.658 | 0.678 | 3.92 | 0.017 | 3.23 |
| InjPress | 5.645 | 2.822 | 0.401 | 7.04 | 0.002 | 1.13 |
| InjTemp | 4.355 | 2.177 | 0.378 | 5.76 | 0.005 | 1.00 |
| CoolTemp | -3.457 | -1.729 | 0.420 | -4.12 | 0.015 | 1.24 |
| Material*InjPress | -0.723 | -0.361 | 0.415 | -0.87 | 0.433 | 1.21 |
| Material*InjTemp | -1.025 | -0.512 | 0.443 | -1.16 | 0.312 | 1.38 |
| Material*CoolTemp | -0.208 | -0.104 | 0.510 | -0.20 | 0.848 | 1.82 |
| InjPress*InjTemp | -0.837 | -0.419 | 0.510 | -0.82 | 0.458 | 1.82 |
| InjPress*CoolTemp | -0.055 | -0.027 | 0.382 | -0.07 | 0.947 | 1.03 |
| InjTemp*CoolTemp | 1.933 | 0.966 | 0.381 | 2.54 | 0.064 | 1.02 |
Model Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
| 1.51005 | 98.02% | 92.57% | 70.86% |
Analysis of Variance
| Source | DF | Adj SS | Adj MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Model | 11 | 451.357 | 41.032 | 17.99 | 0.007 |
| Covariates | 1 | 3.591 | 3.591 | 1.58 | 0.278 |
| MeasTemp | 1 | 3.591 | 3.591 | 1.58 | 0.278 |
| Linear | 4 | 304.587 | 76.147 | 33.39 | 0.002 |
| Material | 1 | 35.053 | 35.053 | 15.37 | 0.017 |
| InjPress | 1 | 113.068 | 113.068 | 49.59 | 0.002 |
| InjTemp | 1 | 75.533 | 75.533 | 33.12 | 0.005 |
| CoolTemp | 1 | 38.666 | 38.666 | 16.96 | 0.015 |
| 2-Way Interactions | 6 | 20.309 | 3.385 | 1.48 | 0.366 |
| Material*InjPress | 1 | 1.732 | 1.732 | 0.76 | 0.433 |
| Material*InjTemp | 1 | 3.045 | 3.045 | 1.34 | 0.312 |
| Material*CoolTemp | 1 | 0.095 | 0.095 | 0.04 | 0.848 |
| InjPress*InjTemp | 1 | 1.538 | 1.538 | 0.67 | 0.458 |
| InjPress*CoolTemp | 1 | 0.012 | 0.012 | 0.01 | 0.947 |
| InjTemp*CoolTemp | 1 | 14.694 | 14.694 | 6.44 | 0.064 |
| Error | 4 | 9.121 | 2.280 | ||
| Total | 15 | 460.478 |
Regression Equation in Uncoded Units
| Strength | = | 52.7 - 1.229 MeasTemp + 10.43 Material + 0.216 InjPress + 0.007 InjTemp - 1.357 CoolTemp - 0.0096 Material*InjPress - 0.0683 Material*InjTemp - 0.0104 Material*CoolTemp - 0.00149 InjPress*InjTemp - 0.00007 InjPress*CoolTemp + 0.01288 InjTemp*CoolTemp |
|---|
Alias Structure
| Factor | Name |
|---|---|
| A | Material |
| B | InjPress |
| C | InjTemp |
| D | CoolTemp |
| Aliases |
|---|
| I - 5.42 ABC + 28.92 ABD - 9.04 ACD - 10.85 BCD + 45.19 ABCD |
| A + 0.15 ABC - 0.77 ABD + 0.24 ACD + 0.29 BCD - 1.21 ABCD |
| B - 0.03 ABC + 0.19 ABD - 0.06 ACD - 0.07 BCD + 0.29 ABCD |
| C - 0.01 ABC + 0.03 ABD - 0.01 ACD - 0.01 BCD + 0.05 ABCD |
| D - 0.05 ABC + 0.25 ABD - 0.08 ACD - 0.09 BCD + 0.39 ABCD |
| AB + 0.04 ABC - 0.24 ABD + 0.07 ACD + 0.09 BCD - 0.37 ABCD |
| AC + 0.06 ABC - 0.32 ABD + 0.10 ACD + 0.12 BCD - 0.50 ABCD |
| AD - 0.09 ABC + 0.47 ABD - 0.15 ACD - 0.18 BCD + 0.74 ABCD |
| BC + 0.09 ABC - 0.47 ABD + 0.15 ACD + 0.18 BCD - 0.74 ABCD |
| BD + 0.02 ABC - 0.08 ABD + 0.03 ACD + 0.03 BCD - 0.13 ABCD |
| CD - 0.01 ABC + 0.07 ABD - 0.02 ACD - 0.03 BCD + 0.11 ABCD |