Interpret the key results for Goodness-of-Fit Test for Poisson

Complete the following steps to interpret a goodness-of-fit test for Poisson. Key output includes the p-value and several graphs.

In This Topic

Step 1: Determine whether the data do not follow a Poisson distribution
Step 2: Examine the difference between observed and expected values for each category

Step 1: Determine whether the data do not follow a Poisson distribution

To determine whether the data do not follow a Poisson distribution, compare the p-value to your significance level (α). Usually, a significance level (denoted as α or alpha) of 0.05 works well. A significance level of 0.05 indicates a 5% risk of concluding that the data do not follow a Poisson distribution when the data do follow a Poisson distribution.

P-value ≤ α: The data do not follow a Poisson distribution (Reject H₀): If the p-value is less than or equal to the significance level, the decision is to reject the null hypothesis and conclude that your data do not follow a Poisson distribution.
P-value > α: You cannot conclude that the data do not follow a Poisson distribution (Fail to reject H₀): If the p-value is larger than the significance level, the decision is to fail to reject the null hypothesis because you do not have enough evidence to conclude that your data do not follow a Poisson distribution.

Method

Frequencies in Observed

Descriptive Statistics

N	Mean
300	0.536667

Observed and Expected Counts for Defects

Defects	Poisson Probability	Observed Count	Expected Count	Contribution to Chi-Square
0	0.584694	213	175.408	8.056
1	0.313786	41	94.136	29.993
2	0.084199	18	25.260	2.086
>=3	0.017321	28	5.196	100.072

Chi-Square Test

Null hypothesis	H₀: Data follow a Poisson distribution
Alternative hypothesis	H₁: Data do not follow a Poisson distribution

DF	Chi-Square	P-Value
2	140.208	0.000

Key Result: P-Value

In these results, the null hypothesis states that the data follow a Poisson distribution. Because the p-value is 0.000, which is less than 0.05, the decision is to reject the null hypothesis. You can conclude that the data do not come from a Poisson distribution.

Step 2: Examine the difference between observed and expected values for each category

Use a bar chart of observed and expected values to determine whether, for each category, the number of observed values differs from the number of expected values. Larger differences between observed and expected values indicate that the data do not follow a Poisson distribution.

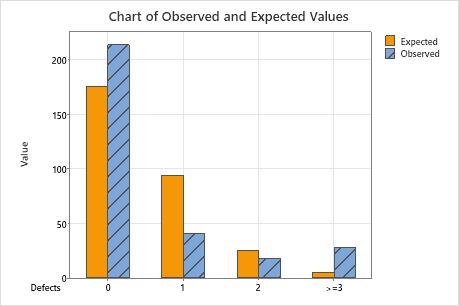
This bar chart indicates that the observed values for 0 defects, 1 defect, and more than 3 defects are different from the expected values. Thus, the bar chart visually confirms what the p-value indicates, which is that the data do not follow a Poisson distribution.