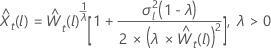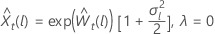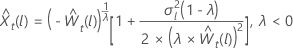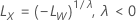에 대한 방법최상의 ARIMA 모형으로 예측

최상의 ARIMA 모형으로 예측 많은 모델을 비교하고 분석 사양에서 기준이 있는 최종 모델을 선택합니다. 최종 ARIMA 모델의 결과에 대한 자세한 내용은 을 ARIMA에 대한 방법 및 공식참조하십시오. 다음 섹션에는 에 고유한 세부 정보가 포함되어 있습니다 최상의 ARIMA 모형으로 예측.

모형 선택

모델 선택은 다음 단계를 사용합니다.

모든 모델에 대한 모델 매개변수를 추정합니다. 모형에 상수가 포함되어 있고 매개변수 추정이 실패하면 상수 항 없이 매개변수를 추정해 보십시오.
각 모델에 대한 정보 기준을 계산합니다. 기본 기준은 수정된 Akaike 정보 기준(AICc)입니다.
정보 기준의 최적 값을 가진 모델에 대한 결과를 생성합니다.

다음 섹션에서는 비계절 및 계절 모델의 선택에 차이가 있는 세부 정보를 설명합니다.

비계절 모델

분석에 대한 사양에는 차이점 보관의 순서가 포함되어 있습니다. 지정된 순서에 대해 프로세스는 분석 사양에서 자동 회귀 및 이동 평균 주문의 모든 조합을 다음과 같은 제한사항으로 평가합니다.

일정한 항을 가진 모델을 적합시키면 후보 모델의 p + q ≤ 9가 있습니다.
상수 항이 없는 모형을 맞추면 후보 모델의 p + q ≤ 10이 됩니다.
d = 2인 모델은 상수 항을 포함하지 않습니다.
모델은 d = 1인 경우에만 ARIMA(0, d, 0)를 평가합니다.

계절 모델

분석의 사양에는 비계절 및 계절적 차이 보관의 순서가 포함되어 있습니다. 지정된 주문의 경우 프로세스는 계절 및 비계절적 자동 회귀 및 이동 평균 주문의 모든 조합을 다음과 같은 제한 사항으로 평가합니다.

일정한 항을 가진 모형을 적합시키면 후보 모형의 p + q + P + Q ≤ 9가 있습니다.
일정한 항이 없는 모형을 적합시키면 후보 모델의 p + q + P + Q ≤ 10이 됩니다.
d + D > 1 인 모델에는 일정한 항이 포함되지 않습니다.
계절 모델을 검색하려면 계절 매개 변수 중 적어도 하나의 순서가 0보다 클 수 있어야 합니다. 검색에 대한 사양에 모든 계절 매개 변수의 순서가 0인 모델이 포함된 경우 검색에 비계절 모델이 포함됩니다.
p, q, P 및 Q 중 적어도 1은 모든 모델에서 0이 아닙니다.

기준

동일한 차이점 보관 순서를 가진 ARIMA 모델을 평가하기 위해 분석에서는 3가지 정보 기준 중 1개를 사용합니다.

AIC(Akaike Information Criterion)
수정된 아카이케 정보 기준(AICc)
베이지안 정보 기준(BIC)

모델에 대한 정보 기준의 계산은 모델에 대한 로그-우도 값을 사용합니다. 로그-우도 값의 계산은 재귀 알고리즘을 사용합니다. 자세한 내용은 Brockwell & Davis (1991)¹

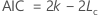
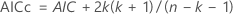
표기법

용어	설명
k	모델의 매개변수 수 상수가 있는 계절 모델의 경우 k = p + q + 2 상수가 없는 계절 모델의 경우 k = p + q + 1 상수가 있는 계절 모델의 경우 k = p + q + P + Q + 2 상수가 없는 계절 모델의 경우 k = p + q + P + Q + 1
L_c	현재 모형의 로그 우도
n	시계열의 표본 크기

Box-Cox 변환

분석을 통해 데이터의 Box-Cox 변환이 가능합니다. 데이터 변환은 모델을 선택하기 전에 발생합니다. 시계열 데이터의 Box-Cox 변환에 대한 자세한 내용은 을 참조하십시오 에 대한 방법 및 공식시계열 대한 Box-Cox 변환.

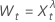분석 결과에는 역변환 예측과 예측의 확률 한계가 포함됩니다. 변환된 시계열의 t^번째 값은 변환에 대한 λ 값에 따라 달라집니다.

λ > 0의 경우
λ = 0의 경우
λ 에 대한 < 0

설명 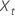는 원래 시계열의 t^번째 값이고 t = 1, ..., n입니다.

그러면 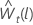변환된 데이터에 대한 원점 t에서 시작하는 l^번째 예측 값이어야 합니다. 그러면 변환된 데이터로부터의 l-단계 예측 분산이어야 합니다. 그런 다음 원래 계열에 대한 t 의 l^번째 예측 값은 λ의 값에 따라 달라집니다 .

예측에 대한 확률 한계의 변환은 Box-Cox 변환의 역을 사용합니다. 확률 한계 계산에 대한 자세한 내용은 을 ARIMA에 대한 방법 및 공식참조하십시오. 확률 상한에 대한 역변환은 낮은 확률 한계에 대한 역변환과 동일합니다. 역변환은 λ의 값에 따라 달라집니다.

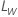설명 는 원래 스케일의 한계이며 는 변환된 스케일의 한계입니다.

랜덤 워크 모델

ARIMA(0, 1, 0) 모델은 상수 항이 있든 없든 랜덤 워크 모델입니다. Minitab 통계 소프트웨어에서는 최상의 ARIMA 모형으로 예측 랜덤 보행 모형을 맞춥니다. 이 명령 통계분석 > 시계열 > ARIMA 에는 하나 이상의 자동 회귀 또는 이동 평균 매개 변수가 필요합니다. 랜덤 보행 모델의 추정 및 확률 한계에는 특정 형태가 있습니다. 예측 가능성, 예측 한계 및 예측 확률 한계에 대한 계산은 모형에 일정한 항이 포함되어 있는지 여부에 따라 달라집니다.

정의:

용어	설명
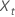	t = 1, ..., n인 시계열에 대한 관측 치
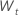	원래 시계열과 첫 번째 차이 데이터,

다음 방정식을 사용하여 상수 없이 모델을 나타냅니다.

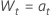
또는

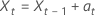
설명 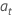는 독립적으로 그리고 동일하게 분포되고 평균 0과 분산 σ², t = 2, ..., n으로 정규 분포 를 따릅니다.

상수가 있는 모델을 나타내는 방정식은 비슷합니다.

또는

우도 값 계산은 다음 방정식을 사용합니다.

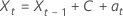
상수 항이 없는 모델

로그 가능성의 형식은 다음과 같습니다.

로그 가능성

설명

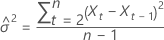
시간 순서에서 시작하여 t + l, l = 1, ..., 150의 예측 값은 다음과 같은 형식을 갖습니다.

예측 값에 대한 100 × (1 – α) 확률 한계 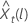의 형식은 다음과 같습니다.

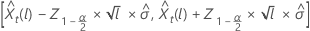
설명 는 표준 정규 분포에서 100개의 ×(1 – α/2)^번째 백분위수를 나타냅니다.

일정한 항을 가진 모델

상수가 있는 모델의 경우 로그 우도에 대한 계산에는 상수 C의 추정이 필요합니다. 첫째, 원본 시리즈와 데이터를 차별화하십시오. 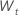t = 2, ..., n에 대한 것입니다. 상수는 표본 평균입니다. 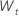의 형식은 다음과 같습니다.

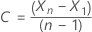
로그 가능성의 형식은 다음과 같습니다.

로그 가능성

설명

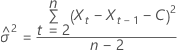
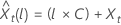
시간 순서에서 시작하여 t + l, l = 1, ..., 150의 예측 값은 다음과 같은 형식을 갖습니다.

예측 값에 대한 100 × (1 – α) 확률 한계 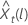의 형식은 다음과 같습니다.

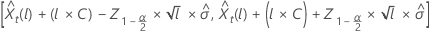
설명 는 표준 정규 분포에서 100개의 ×(1 – α/2)^번째 백분위수를 나타냅니다.

¹ Brockwell, P. J. & Davies, R., A. (1991)의 섹션 8.6을 참조하십시오. ARMA 모델에 대한 추정. 안으로: 시계열 이론과 방법. 통계의 스프링거 시리즈. 스프링어, 뉴욕, 뉴욕. https://doi.org/10.1007/978-1-4419-0320-4_1.