한 마케팅 분석가가 ARIMA 모델을 사용하여 샴푸 제품의 판매에 대한 단기 예측을 생성하려고 합니다. 분석가는 이전 삼 년간의 판매 데이터를 수집합니다. 시계열 그림에서 분석가는 데이터 추세가 더 높다는 것을 알 수 있습니다. 이 패턴은 데이터의 평균이 고정되어 있지 않음을 나타냅니다. 분석가는 증강 Dickey-Fuller 테스트를 수행하여 ARIMA 모델에 포함할 비계절적 차이 보관의 순서를 결정합니다. ARIMA 모델에 대한 자세한 내용은 을 참조하십시오 ARIMA 개요.
- 표본 데이터 샴푸판매.MWX를 엽니다.
- 을 선택합니다.
- 시계열에서 영업를 입력합니다.
- 확인을 선택합니다.
결과 해석
이 결과에서 2.29045의 검정 통계량은 -2.96053의 임계 값보다 큽니다. 결과가 데이터가 고정되어 있지 않다는 귀무 가설을 기각하지 못하기 때문에 테스트의 권장 사항은 데이터를 고정시키기 위해 일차 차이점 보관을 고려하는 것입니다.
방법
| 회귀 모델의 항에 대한 최대 지연 순서 | 9 |
|---|---|
| 지연 순서 선택 기준 | 최소 AIC |
| 추가 항 | 상수 |
| 선택한 지연 순서 | 4 |
| 사용된 행 | 36 |
증대된 Dickey-Fuller 검정
| 귀무 가설: | 데이터는 고정되지 않습니다. |
|---|---|
| 대립 가설: | 데이터는 고정되어 있습니다. |
| 검정 통계량 | P-값 | 추천 |
|---|---|---|
| 2.29045 | 0.999 | 검정 통계 > -2.96053의 임계값. |
| 유의 수준 = 0.05 | ||
| 귀무 가설을 거부하지 않습니다. | ||
| 데이터를 고정하기 위해 차분 계산을 고려하십시오. |
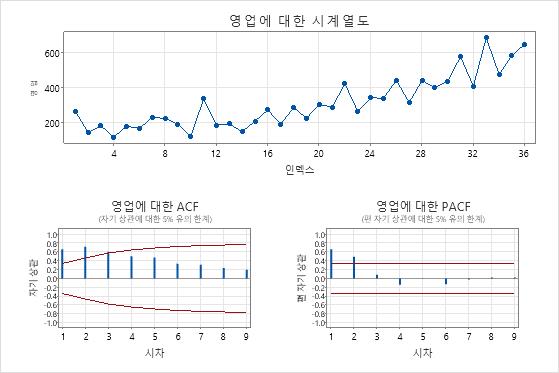
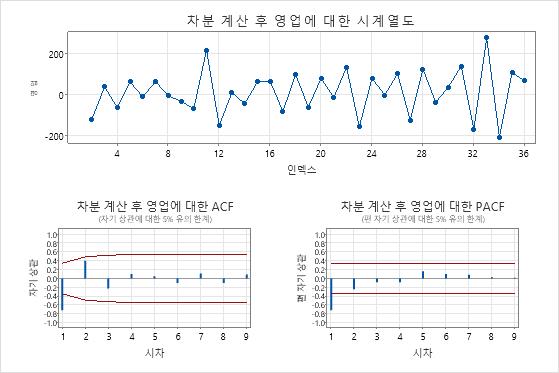
시계열 그림은 차이점 보관의 결과를 보여 줍니다. 이 결과에서 원본 데이터의 시계열 그림은 명확한 추세를 보여줍니다. 차이난 데이터의 시계열 그림은 연속적인 값 간의 차이를 보여줍니다. 차이가 있는 데이터는 점들이 변동에서 명백한 패턴 없이 수평 경로를 따르기 때문에 고정되어 나타납니다.
ACF 플롯은 또한 차이점 보관의 효과를 보여줍니다. 이 결과에서 원본 데이터의 ACF 플롯은 지연에 걸쳐 천천히 감소된 스파이크를 보여줍니다. 이 패턴은 데이터가 고정되어 있지 않음을 나타냅니다. 차이 데이터의 ACF 플롯에서 0과 유의하게 다른 스파이크는 지연 1에 있습니다.
이 결과에서 시계열 플롯과 ACF 플롯은 테스트 결과를 확인합니다. 따라서 합리적인 접근 방식은 데이터를 차이로 만든 다음 자동 회귀 및 이동 평균 모델을 적합시켜 예측을 수행하는 것입니다.