1단계. 모형의 성분 수 확인
PLS의 목적은 예측 능력이 우수하고 성분의 수가 적절한 모형을 선택하는 것입니다. PLS 모형을 적합시키는 경우, 교차 검증을 수행하여 모형의 최적 성분 수를 결정하는 데 도움을 받을 수 있습니다. 교차 검증을 사용할 경우, Minitab은 예측 R2 값이 가장 큰 모형을 선택합니다. 교차 검증을 사용하지 않는 경우, 모형에 포함할 성분의 수를 지정하거나 기본 성분 수를 사용할 수 있습니다. 기본 성분 수는 10개 또는 데이터의 예측 변수 수 중 더 적은 값입니다. 방법 표를 살펴보고 Minitab이 모형에 구성 요소를 몇 개 포함했는지 확인하십시오. 모형 선택 그림도 살펴볼 수 있습니다.
PLS를 사용하는 경우, 예측 변수와 반응값의 변동성을 충분히 설명하는 모형 중 가장 적은 수의 성분이 포함된 모형을 선택하십시오 데이터에 가장 적합한 성분 수를 결정하려면 X-분산, R2 및 예측 R2 값을 포함한 모형 선택 표를 살펴보십시오. 예측 R2은 모형의 예측 능력을 나타내며, 교차 검증을 수행하는 경우에만 표시됩니다.
경우에 따라 Minitab에서 처음 선택된 것과 다른 모형을 사용하기로 결정할 수도 있습니다. 교차 검증을 사용한 경우 R2와 예측 R2를 비교하십시오. Minitab이 예측 R2를 조금만 감소시키는 모형에서 성분 2개를 제거하는 예에 대해 생각해 보십시오. 이 경우 예측 R2이 약간만 작아지기 때문에 모형은 과다 적합이 아니며 데이터에 더 적합하다고 결정할 수 있습니다.
예측 R2이 R2보다 상당히 작으면 모형이 과다 적합하다는 것을 나타낼 수도 있습니다. 모집단에서 중요하지 않은 효과에 대한 항이나 성분을 추가할 경우 과다 적합 모형이 발생할 수 있습니다. 모형이 표본 데이터에 따라 조정되므로, 모집단에 대해 예측 시 유용하지 않을 수도 있습니다.
교차 검증을 사용하지 않는 경우 모형 선택 표에서 x-분산 값을 조사하여 반응의 분산이 각 모형으로 얼마나 설명되는지 확인할 수 있습니다.
방법
| 교차 검증 | 단일 관측치 제거법 |
|---|---|
| 계산할 성분 | 설정 |
| 평가된 성분 수 | 10 |
| 선택된 성분 수 | 4 |
방법
| 교차 검증 | 없음 |
|---|---|
| 계산할 성분 | 설정 |
| 계산된 성분 수 | 10 |
주요 결과: 성분 수
이 결과에서 첫 번째 방법 표에서는 교차 검증이 사용되고 성분이 4개인 모형이 선택되었습니다. 두 번째 방법 표에서는 교차 검증이 사용되지 않았습니다. Minitab은 성분이 10개(기본값)인 모형을 사용합니다.
향에 대한 모형 선택 및 검증
| 성분 | X 분산 | 오차 | R-제곱 | PRESS | R-제곱(예측) |
|---|---|---|---|---|---|
| 1 | 0.158849 | 14.9389 | 0.637435 | 23.3439 | 0.433444 |
| 2 | 0.442267 | 12.2966 | 0.701564 | 21.0936 | 0.488060 |
| 3 | 0.522977 | 7.9761 | 0.806420 | 19.6136 | 0.523978 |
| 4 | 0.594546 | 6.6519 | 0.838559 | 18.1683 | 0.559056 |
| 5 | 5.8530 | 0.857948 | 19.2675 | 0.532379 | |
| 6 | 5.0123 | 0.878352 | 22.3739 | 0.456988 | |
| 7 | 4.3109 | 0.895374 | 24.0041 | 0.417421 | |
| 8 | 4.0866 | 0.900818 | 24.7736 | 0.398747 | |
| 9 | 3.5886 | 0.912904 | 24.9090 | 0.395460 | |
| 10 | 3.2750 | 0.920516 | 24.8293 | 0.397395 |
주요 결과: X-분산, R-제곱, R-제곱(예측)
이 결과에서 Minitab은 예측 R2 값이 약 56%인 4-성분 모형을 선택했습니다. x-분산을 토대로 4-성분 모형은 예측 변수의 분산을 60% 가까이 설명합니다. 성분 수가 증가할수록 R2 값이 커지지만, 예측 R2가 작아져서 성분이 더 많은 모형이 과대 적합할 수 있음을 나타냅니다.
2단계. 데이터에 특이치 또는 레버리지 점이 있는지 확인
모형이 데이터에 적합한지 판단하려면 그림을 살펴보고 특이치, 레버리지 점 및 기타 패턴을 찾아봐야 합니다. 데이터에 특이치나 레버리지 점이 많이 포함되어 있는 경우 모형의 예측이 올바르지 않을 수 있습니다.
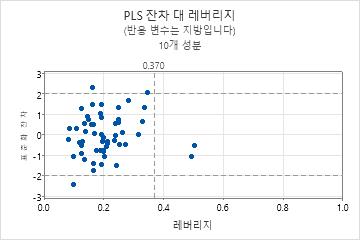
- 특이치: 표준화 잔차가 큰 관측치는 그림의 가로 기준선 밖에 있습니다.
- 레버리지 점: 레버리지 값이 있는 관측치의 x-점수는 0에서 멀고 세로 기준선의 오른쪽에 있습니다.
잔차 대 레버리지 그림에 대한 자세한 내용은 부분 최소 제곱법에 대한 그래프에서 확인하십시오.
- 모형이 데이터를 잘 적합하거나 예측하지 않을 수 있음을 나타내는 점의 비선형 패턴.
- 교차 검증을 수행하는 경우, 레버리지 점을 나타내는 적합치 및 교차 검증된 값의 큰 차이.

3단계. 검정 데이터 집합을 사용하여 PLS 모형 검증
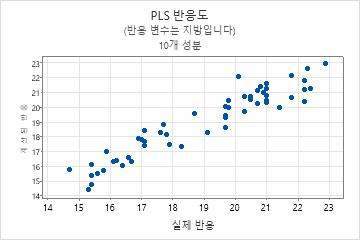
PLS 회귀 분석은 종종 2단계로 진행됩니다. 때때로 교육이라고 하는 첫 번째 단계에는 표본 데이터 집합에 대한 PLS 회귀 모형 계산이 포함됩니다. 두 번째 단계에는 검정 데이터 집합이라고 하는 다른 데이터 집합을 사용하여 모형을 검증합니다. 검정 데이터 집합을 사용하여 모형을 검증하려면 예측 하위 대화 상자에 검증 데이터 열을 입력합니다. Minitab에서는 검정 데이터 집합의 각 관측치에 대해 새 반응 값을 계산하고 예측 반응 값을 실제 반응 값과 비교합니다. Minitab에서는 비교 결과를 토대로 모형이 새 반응 값을 예측하는 능력을 나타내는 검정 R2을 계산합니다. 검정 R2가 높을수록 모형의 예측 능력이 더 우수함을 나타냅니다.
교차 검증을 사용하는 경우 검정 R2과 예측 R2을 비교해야 합니다. 이상적인 경우 두 값은 비슷합니다. 검정 R2이 예측 R2보다 상당히 작으면 교차 검증이 모형의 예측 능력에 대해 지나치게 낙관적이거나 두 데이터 표본이 다른 모집단에서 추출된 것임을 나타냅니다.
검정 데이터 집합에 반응 값이 포함되어 있지 않으면 Minitab에서 검정 R2을 계산하지 않습니다.
지방에 대한 모델을 사용한 새로운 관측치에 대한 예측 반응
| 행 | 적합치 | SE 적합치 | 95% CI | 95% PI |
|---|---|---|---|---|
| 1 | 18.7372 | 0.378459 | (17.9740, 19.5004) | (16.8612, 20.6132) |
| 2 | 15.3782 | 0.362762 | (14.6466, 16.1098) | (13.5149, 17.2415) |
| 3 | 20.7838 | 0.491134 | (19.7933, 21.7743) | (18.8044, 22.7632) |
| 4 | 14.3684 | 0.544761 | (13.2698, 15.4670) | (12.3328, 16.4040) |
| 5 | 16.6016 | 0.348485 | (15.8988, 17.3044) | (14.7494, 18.4538) |
| 6 | 20.7471 | 0.472648 | (19.7939, 21.7003) | (18.7861, 22.7080) |
주요 결과: 검정 R 2
이 결과에서 검정 R2은 약 76%입니다. 원래 데이터 집합에 대한 예측 R2은 약 78%입니다. 이 두 값은 유사하므로, 모형의 예측 능력이 충분하다는 결론을 내릴 수 있습니다.
