을 실행합니다. 결과에서대체 모델 선택을
클릭합니다.
참고
이 명령은 예측 분석 모듈에서 사용할 수 있습니다. 모듈을 활성화하는 방법에 대한 자세한 내용은 여기를 클릭하십시오.
개요
Minitab 통계 소프트웨어는 최적성 기준의 최적 값을 사용하여 모형에 대한 결과를 생성합니다. 기준은 선택에 따라 최소 제곱 오차 또는 최소 절대 편차입니다. Minitab을 사용하면 최적 모형을 식별하는 시퀀스에서 다른 모형들을 탐색할 수 있습니다. 일반적으로 다음 두 가지 이유 중 하나로 대체 모델을 선택합니다.
- 분석에서 선택하는 모형은 기준이 개선되는 패턴의 일부입니다. 일반적으로 가능한 한 예측 정확도를 가진 모델에서 예측을 수행하려고 합니다.
- 분석에서 선택하는 모형은 기준이 비교적 평평한 패턴의 일부입니다. 유사한 모형 요약 통계량을 가진 하나 이상의 모형은 최적 모형보다 훨씬 적은 기저 함수를 갖습니다. 일반적으로 기저 함수가 더 적은 모형은 각 예측 변수가 반응 값에 미치는 영향을 더 명확하게 보여줍니다. 더 작은 모형에 대한 예측 정확도의 차이가 무시할 수 있는 경우 더 작은 모형을 사용하여 반응과 예측 변수 간의 관계를 평가할 수 있습니다.
예를 들어, 다음 그림은 20개의 기저 함수가 있는 트리에 대한 결과와 함께 제공됩니다. 시퀀스의 다른 모델은 유사한R2 값을 갖는다.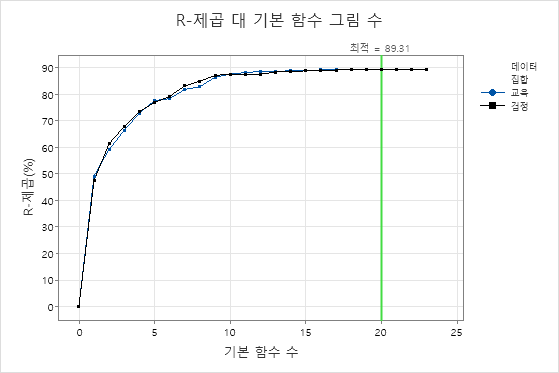

10개의 기저 함수를 갖는 모델의R2 값은 20개의 기저 함수를 갖는 모델만큼 높습니다. 일반적으로 기저 함수가 더 적은 모형은 각 예측 변수가 반응 값에 미치는 영향을 더 명확하게 보여줍니다. 훨씬 더 작은 모형에서 예측 정확도의 감소가 무시할 수 있는 경우 훨씬 더 작은 모형을 사용하여 반응과 예측 변수 간의 관계를 평가할 수 있습니다.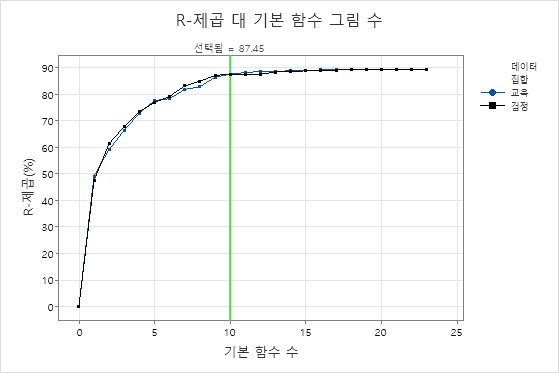

대체 모델에 대한 기준 값 외에도 모델의 복잡성과 다른 지역의 유용성을 비교할 수도 있습니다. 분석가가 다른 트리와 비교할 때 성능을 희생하지 않는 특정 트리를 선택하는 이유에 대한 다음 예를 생각해 보십시오.
- 분석가는 가장 중요한 변수를 더 명확하게 볼 수 있는 더 작은 모형을 선택합니다.
- 분석에서 모형을 선택하는 이유는 기저 함수가 다른 모형의 변수보다 측정하기 쉬운 변수에 대한 함수이기 때문입니다.
- 분석가가 모형을 선택하는 이유는 예측 변수의 특정 영역에 관심이 있기 때문입니다.
분석 수행
출력에서 선택합니다 대체 모델 선택 . 기저 함수 수에 대한 기준의 플롯과 단계를 요약하는 테이블을 보여주는 대화 상자가 열립니다.
기준 비교
대체 모델을 선택하려면 그래프에서 점을 선택하거나 테이블에서 행을 선택합니다. 해당 모델에 대한 결과를 만들려면 선택합니다 결과 표시 .
결과가 표시되면 모델에서 예측을 수행하도록 선택할 예측 수 있습니다. 자세한 내용은 MARS® 회귀 분석에 대한 새로운 결과 예측를 참조하십시오.
팁
두 개의 분석 또는 보고서 결과를 비교하려면 탐색기에서 두 번째 항목을 마우스 오른쪽 단추로 클릭하고 분할 보기에서 열기을(를) 선택합니다.
