다중 비교 검정
k > 2 표본에 대한 다중 비교 구간
다음과 같이 설정합니다. 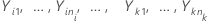 를 k > 2개의 독립 표본으로 설정합니다. 각 표본은 독립적이고 평균이
를 k > 2개의 독립 표본으로 설정합니다. 각 표본은 독립적이고 평균이 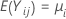 이고 분산이
이고 분산이  인 동일한 분포를 따릅니다. 또한 공통 첨도가 다음과 같은 모집단에서 표본이 추출되었다고 가정합니다.
인 동일한 분포를 따릅니다. 또한 공통 첨도가 다음과 같은 모집단에서 표본이 추출되었다고 가정합니다. 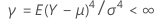
그리고 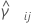 를 다음과 같이 지정되는 표본 (i, j)의 쌍에 대한 합동 첨도 추정량으로 설정합니다.
를 다음과 같이 지정되는 표본 (i, j)의 쌍에 대한 합동 첨도 추정량으로 설정합니다.
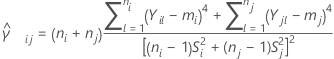
다음과 같이 설정합니다. 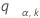 를 동일한 분포를 따르는 k개의 독립적인 표준 정규 랜덤 변수 범위의 상위 한 점으로 설정합니다. 즉,
를 동일한 분포를 따르는 k개의 독립적인 표준 정규 랜덤 변수 범위의 상위 한 점으로 설정합니다. 즉, 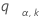 는 다음을 충족합니다.
는 다음을 충족합니다.
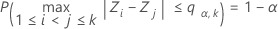
여기서 Z1, ..., Zk는 동일한 분포를 따르는 독립적인 표준 정규 랜덤 변수입니다. Barnard(1978)는 정규 범위의 분포 함수 계산을 위해 16점 가우스 구적법에 기반한 간단한 숫자 알고리즘을 제공합니다.
다중 비교 절차는 다음 구간의 한 쌍 이상이 겹치지 않을 경우에만 분산 동일성(분산의 동질성이라고도 함)의 귀무 가설을 기각합니다.
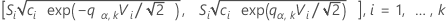
설명:
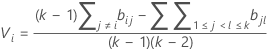
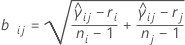
여기서 ri = (ni - 3) / ni입니다.
위의 구간을 다중 비교 구간 또는 MC 구간이라고 합니다. 각 표본에 대한 MC 구간은 상위 모집단의 표준 편차에 대한 신뢰 구간으로 해석할 수 없습니다. Hochberg et al. (1982)은 평균을 비교하는 데 사용되는 이와 유사한 구간을 "확실성 구간"이라고 지칭합니다. 여기에 지정된 MC 구간은 다중 표본 설계에 대한 표준 편차 또는 설계를 비교하는 데만 유용합니다. 전체 다중 비교 검정이 유의한 경우 겹치지 않는 구간에 해당하는 표준 편차는 통계적으로 서로 다릅니다. (이러한 구간에 대한 추가 정보는 다중 비교 방법에 대한 백서를 참조하십시오.)
k =2 표본에 대한 다중 비교 구간
표본이 두 개뿐인 경우 다중 비교 구간은 다음과 같습니다.

여기서 zα / 2는 표준 정규 분포의 상위 α / 2 백분위수 점이고, ci = ni / ni - zα / 2이며 Vi는 다음 공식으로 지정됩니다.
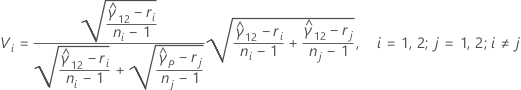
검정에 대한 p-값
설계에 표본이 2개 있는 경우 Minitab에서는 두 표본 분산 검정에 대한 Bonett의 방법 및 귀무 가설에서의 비율, Ρo = 1을 사용하여 다중 비교에 대한 p-값을 계산합니다.
설계에 k > 2개의 표본이 있는 경우, Pi j를 표본의 모든 쌍(i, j )에 대한 검정의 p-값을 설정하십시오. 분산 동일성에 대한 전체 검정으로서의 다중 비교 절차에 대한 p-값은 다음과 같이 계산됩니다.

시뮬레이션 및 Pi j를 계산하기 위한 상세한 알고리즘 등 자세한 내용은 시뮬레이션 및 Bonett의 방법에 대한 기타 정보가 포함되어 있는 Bonett의 방법 백서를 참조하십시오.
표기법
| 용어 | 설명 |
|---|---|
| ni | 표본 i의 관측치 수 |
| Y i l | 표본 i의 j번째 관측치 |
| mi | 표본 i에 대한 절사 평균 - 절사 비율:  |
| k | 표본 개수 |
| Si | 표본 i의 표준 편차 |
| α | 검정의 유의 수준 = 1 - (신뢰 수준 / 100) |
| Ci | 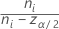 |
| Zα / 2 | 표준 정규 분포의 상위 α/2 백분위수 점 |
| ri |  |
Levene의 검정 통계량
Minitab은 Levene의 검정에 대한 검정 통계량과 p-값을 표시합니다. 귀무 가설은 분산이 같다는 것이고 대립 가설은 분산이 같지 않다는 것입니다. 정규 분포 여부에 상관없이 계량형 분포의 데이터인 경우 Levene의 검정을 사용합니다.
Levene의 검정에 대한 계산 방법은 Brown and Forsythe (1974)이 개발한 Levene의 절차(Levene, 1960)를 수정한 것입니다. 이 방법에서는 표본 평균 대신 표본 중위수로부터 관측치까지의 거리를 사용합니다. 표본 평균 대신 표본 중위수를 사용하면 표본 크기가 작을수록 보다 로버스트한 검정이 수행되며 절차가 점근적으로 특정 분포에 종속되지 않습니다. p-값이 α-수준보다 작으면 분산이 같다는 귀무 가설을 기각하십시오.
수식
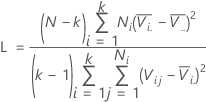
- H. Levene (1960). Contributions to Probability and Statistics. Stanford University Press, CA.
- M. B. Brown and A. B. Forsythe (1974). "Robust tests for the equality of variance," Journal of the American Statistical Association, 69, 364-367.
표기법
| 용어 | 설명 |
|---|---|
| Vij |  |
| i | 1, ..., k |
| j | 1, ..., ni |
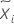 | 중위수 |
Bartlett의 검정 통계량
Minitab은 Bartlett 검정에 대한 검정 통계량과 p-값을 표시합니다. 수준이 두 개뿐인 경우 Minitab에서는 Bartlett의 검정 대신 F-검정을 수행합니다. 이 검정의 경우, 귀무 가설은 분산이 같다는 것이고 대립 가설은 분산이 같지 않다는 것입니다. 데이터를 정규 분포에서 얻은 경우에는 Bartlett의 검정을 사용합니다. 데이터가 정규 분포를 벗어날 경우 Bartlett의 검정은 로버스트하지 않습니다.
Bartlett의 검정 통계량은 자유도를 기반으로 각 표본 분산의 가중 산술 평균과 가중 기하 평균을 계산합니다. 평균의 차이가 클수록 표본의 분산이 같지 않을 확률이 높습니다. B는 자유도가 k - 1인 χ2 분포를 따릅니다. p-값이 α-수준보다 작으면 분산이 같다는 귀무 가설을 기각하십시오.
공식
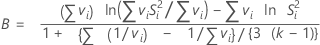
표기법
| 용어 | 설명 |
|---|---|
| si2 |  |
| k | 표본 개수 |
| vi | ni - 1 |
| ni | i번째 요인 수준에서의 관측치 수 |
F-검정 통계량
수준이 두 개뿐인 경우 Minitab에서는 Bartlett의 검정 대신 F-검정을 수행합니다. 귀무 가설은 분산이 같다는 것이고 대립 가설은 분산이 같지 않다는 것입니다. 데이터가 정규 분포를 따르는 경우 F-통계량을 사용하십시오.
p-값이 α-수준보다 작으면 분산이 같다는 귀무 가설을 기각하십시오.
공식
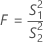
p-값을 위한 공식
- 보다 작음 대립 가설을 사용하는 단측 검정의 경우, p-값은 자유도가 DF1 및 DF2인 F-분포에서 관측된 값보다 작거나 같은 F-통계량을 얻을 확률과 같습니다.
- 비율이 1보다 작은 양측 검정의 경우, p-값은 자유도가 DF1 및 DF2인 F-분포에서 관측된 값보다 작은 F-곡선 아래 면적의 두 배와 같습니다.
- 비율이 1보다 큰 양측 검정의 경우, p-값은 자유도가 DF1 및 DF2인 F-분포에서 관측된 값보다 큰 F-곡선 아래 면적의 두 배와 같습니다.
- 보다 큼 대립 가설을 사용하는 단측 검정의 경우, p-값은 자유도가 DF1 및 DF2인 F-분포에서 관측된 값보다 크거나 같은 F-통계량을 얻을 확률과 같습니다.
표기법
| 용어 | 설명 |
|---|---|
| S12 | 표본 1의 분산 |
| S22 | 표본 2의 분산 |
| n1 - 1 | 분자의 자유도 |
| n2 - 1 | 분모의 자유도 |
표준 편차
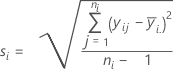
표기법
| 용어 | 설명 |
|---|---|
| yij | i번째 요인 수준에서의 관측치 |
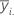 | i번째 요인 수준에서 관측치의 평균 |
| ni | i번째 요인 수준에서의 관측치 수 |
Bonferroni 신뢰 구간
Minitab에서는 Bonferroni 방법을 사용하여 표준 편차에 대한 신뢰 구간을 계산합니다. 신뢰 구간은 모집단 모수, 이 경우 표준 편차가 포함될 수 있는 값의 범위입니다.
표준 신뢰 구간은 신뢰 수준 1 – α / 2를 사용하여 계산됩니다. Bonferroni 방법은 각각의 개별 신뢰 구간에 대해 신뢰 수준 1 – α / 2p를 사용합니다(여기서 p는 요인 및 수준 조합의 수입니다). 이 방법을 사용하면 신뢰 구간 집합의 신뢰 수준이 적어도 1 – α가 됩니다. Bonferroni 방법은 더 보수적인(넓은) 신뢰 구간을 제공하므로, 제1종 오류의 확률이 감소합니다.
