이 항목의 내용
공차 구간 방법
- 로그 정규 분포
- 감마 분포
- 지수 분포
- 최소 극단값 분포
- Weibull 분포
- 최대 극단값 분포
- 로지스틱 분포
- 로그 로지스틱 분포
일반 정의
X 1, X 2, ..., X n을 계량형 분포에서 추출한 크기 n의 랜덤 표본을 기반으로 한 순서 통계량이라고 정의합니다.
분포 함수를 크기가 1보다 크거나 같은 모수 공간에서 Ω에 대한 F(x;θ)로 정의합니다.
L < U를 α 및 P(0 < α < 1, 0 < P < 1) 값이 지정된 경우 Ω의 모든 θ에 대해 다음 조건을 충족하는 표본을 기반으로 하는 두 통계량으로 정의합니다.
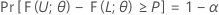
그런 다음, 구간 [ L, U]은 내용 = P x 100%이고 신뢰 수준 = 100(1 - α)%인 양측 공차 구간입니다. 이러한 구간을 양측 (1 - α, P) 공차 구간이라고 합니다. 예를 들어, α = 0.10이고 P = 0.85인 경우 생성되는 구간을 양측 (90%, 0.85) 공차 구간이라고 합니다.
L = –∞이고 U < +∞인 경우 구간 (-∞, U]을 단측 (1 – α, P) 공차 상한이라고 합니다. L > -∞이고 U = +∞인 경우 구간 [L, +∞)을 단측 (1 – α, P) 공차 하한이라고 합니다.
- 단측 (1 – α, P) 공차 하한은 또한 단측 (P, 1 – α) 공차 상한입니다.
- 데이터 분포의 (1 – P)번째 백분위수의 단측 (1 – α )100% 신뢰 하한은 또한 단측 (1 – α, P) 공차 하한입니다. 마찬가지로, 데이터 분포의 P번째 백분위수의 단측 (1 – α )100% 신뢰 상한은 또한 (1 – α , P) 공차 상한입니다.
- L과 U가 단측 (1 – α/2 , (1 + P )/2) 공차 하한 및 상한인 경우 [ L, U ]는 대략적인 양측 (1 – α, P ) 공차 구간입니다. 이 방법은 양측 공차 구간을 직접 얻을 수 없는 경우 사용할 수 있습니다. 그 결과 일반적으로 보수적인 양측 공차 구간이 생성됩니다. Guenther1 및 Hahn and Meeker2를 참조하십시오.
- Guenther, W. C. (1972). Tolerance intervals for univariate distributions. Naval Research Logistics, 19: 309–333.
- Hahn G. J. and Meeker W. Q. (1991). Statistical Intervals: A Guide for Practitioners John Wiley & Sons, New York.
계량형 분포에 대한 정확한 비모수 공차 구간
Minitab에서는 정확한 (1 – α, P) 비모수 공차 구간을 계산하며, 여기서 1 – α은 신뢰 수준이고 P는 범위(구간 내 모집단의 목표 최소 백분율)입니다. 공차 구간에 대한 비모수 방법은 분포를 사용하지 않는 방법입니다. 즉, 비모수 공차 구간은 표본의 상위 모집단에 종속되지 않습니다. Minitab에서는 단측과 양측 구간 모두에 대해 정확한 방법을 사용합니다.
X 1, X 2 , ... , X n 을 계량형 분포를 따르는 모집단 F(x;θ)에서 추출한 랜덤 표본의 순서 통계량이라고 설정합니다. 그런 다음, Wilks1, 2 및 Robbins3의 결과를 기반으로 다음과 같이 표시할 수 있습니다.

여기서・B는 모수가・a・=・r・및・b・=・n・–・s・+・1인・베타・분포의・누적분포함수를・나타냅니다.・따라서・(・Xr・・,・Xs・)는・구간・범위에・상위・모집단,・F(x;θ)의・분포와・독립적인,・모수・값을・알고・있는・베타・분포가・포함되기・때문에・분포와・관계・없는・공차・구간입니다.・
단측 구간
k를 다음 조건을 만족하는 가장 큰 정수라고 설정합니다.

여기서 Y는 모수가 n 및 1 – P인 이항 랜덤 변수입니다. 단측 (1 – α, P) 공차 하한이 Xk 로 지정될 수 있습니다(Krishnamoorthy and Mathew4 참조). 마찬가지로, 단측 (1 – α, P) 공차 상한은 X n - k +1로 지정됩니다. 두 경우 모두 실제 또는 유효 범위는 P(Y > k)로 지정됩니다.
양측 구간
k를 다음 조건을 만족하는 가장 작은 정수라고 설정합니다.

여기서 V는 모수가 n 및 P인 이항 랜덤 변수입니다. 따라서 다음과 같습니다.
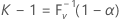
여기서 F V -1(x)는 V의 역 누적분포함수입니다. 양측 (1 – α, P) 공차 구간이 ( Xr , Xs )로 지정될 수 있습니다(Krishnamoorthy and Mathew4 참조). Minitab에서는 r = (n – k + 1) / 2인 s = n - r + 1를 선택합니다. r와 s는 가장 가까운 정수로 내림됩니다. 실제 또는 유효 범위는 P(V < k – 1)로 정의됩니다.
표기법
| 용어 | 설명 |
|---|---|
| 1 – α | 공차 구간의 신뢰 수준 |
| P | 공차 구간의 범위(구간 내 모집단의 목표 최소 백분율) |
| n | 표본의 관측치 수 |
- Wilks, S. S. (1941). Sample size for tolerance limits on a normal distribution. The Annals of Mathematical Statistics, 12, 91–96.
- Wilks, S. S. (1941). Statistical prediction with special reference to the problem of tolerance limits. The Annals of Mathematical Statistics, 13, 400–409.
- Robbins, H. (1944). On distribution-free tolerance limits in random sampling. The Annals of Mathematical Statistics, 15, 214–216.
- Krishnamoorthy, K. and Mathew, T. (2009). Statistical Tolerance Regions: Theory, Applications, and Computation. Wiley, Hoboken, NJ.
로그 정규 분포
- Minitab이 데이터의 자연 로그를 취합니다.
- Minitab이 정규 분포에 대한 공차 구간 절차를 사용하여 변환된 데이터에 대한 공차 구간을 계산합니다.
- Minitab이 이전 단계에서 얻은 공차 구간의 한계를 거듭제곱하여 구간을 원래 데이터의 척도로 변환합니다.
감마 분포에 대한 근사적인 공차 구간
감마 분포에 대한 공차 구간에서는 정규 분포에 대한 근사를 사용합니다. Krishnamoorthy, et al.은 근사가 정확한 결과를 제공한다는 것을 보여주는 시뮬레이션 연구를 수행합니다. 계산 과정은 다음과 같습니다.
- Minitab이 데이터의 세제곱근을 취합니다.
- Minitab이 정규 분포에 대한 공차 구간 절차를 사용하여 변환된 데이터에 대한 공차 구간을 계산합니다.
- Minitab이 이전 단계에서 얻은 공차 구간의 한계를 거듭제곱하여 구간을 원래 데이터의 척도로 변환합니다.
- Krishnamoorthy K., Mathew T and Mukherjee S (2008). Normal based methods for a Gamma distribution: prediction and tolerance intervals and stress-strength reliability. Technometrics, 50, 69—78.
지수 분포
Minitab에서는 정확한 (1 – α, P) 공차 구간을 계산하며, 여기서 1 – α은 신뢰 수준이고 P는 범위(구간 내 모집단의 목표 최소 비율)입니다. 단측 공차 한계와 양측 공차 구간의 계산 공식은 서로 다릅니다.
단측 지수 공차 한계
하한의 계산 공식은 다음과 같습니다.
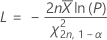
상한의 계산 공식은 다음과 같습니다.

양측 지수 신뢰 구간
Minitab에서는 Newton의 방법을 사용하여 다음 방정식을 풉니다. 자세한 내용은 Fernandez1를 참조하십시오.
양측 구간의 계산 공식은 다음과 같습니다.

설명:

이며 k 1의 값은 이 방정식의 해에 종속됩니다.

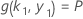
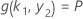
설명:
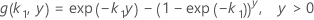
표기법
| 용어 | 설명 |
|---|---|
| n | 표본 크기 |
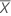 | 표본 평균 |
| P | 구간 내 모집단의 목표 최소 비율 |
 | 자유도가 2n인 카이-제곱 분포의 α번째 백분위수 |
| α | 1 − 신뢰 수준 |
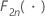 | 자유도가 2n인 카이-제곱 분포의 누적분포함수 |
- Fernandez, Arturo J. (2010). Two-sided tolerance intervals in the exponential case: Corrigenda and generalizations. Computational Statistics and Data Analysis, 54, 151—162.
최소 극단값 분포
Minitab에서는 Lawless1를 기반으로 정확한 (1 – α, P) 공차 구간을 계산하며, 여기서 1 – α은 신뢰 수준이고 P는 범위(구간 내 모집단의 목표 최소 백분율)입니다.
정확한 단측 최소 극단값 공차 한계
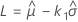
설명:


사용
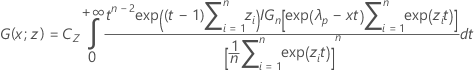
설명:

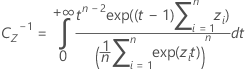
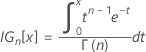
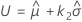
k 2 값은 k 1 계산 공식에서 α를 1 − α로, P를 1 − P로 바꾸어서 계산합니다.
근사적인 양측 최소 극단값 공차 한계
근사적인 양측 구간을 계산하려면 단측 공차 한계의 계산 공식에서 α를 α/2, P를 (P + 1)/2로 바꾸십시오.
표기법
| 용어 | 설명 |
|---|---|
 | 극단값 분포의 위치 모수의 최대우도 추정치 |
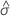 | 극단값 분포의 척도 모수의 최대우도 추정치 |
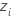 | 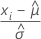 , 최소 극단값 분포의 위치 및 척도 모수의 MLE 추정치를 기반으로 한 중앙 관측치 , 최소 극단값 분포의 위치 및 척도 모수의 MLE 추정치를 기반으로 한 중앙 관측치 |
| t | 자유도가 n − 1이고 비중심 모수가 δP 인 비중심 t-분포의 α번째 백분위수 |
| 1 - α | 공차 구간의 신뢰 수준 |
| P | 공차 구간의 범위(구간 내 모집단의 목표 최소 백분율) |
| n | 표본의 관측치 수 |
- Lawless, J. F. (1975). Construction of tolerance bounds for the extreme-value and the Weibull distribution. Technometrics, 17, 255—261.
Weibull 분포
- Minitab이 데이터의 자연 로그를 취합니다.
- Minitab이 최소 극단값 분포에 대한 공차 구간 절차를 사용하여 변환된 데이터에 대한 공차 구간을 계산합니다.
- Minitab이 이전 단계에서 얻은 공차 구간의 한계를 거듭제곱하여 구간을 원래 데이터의 척도로 변환합니다.
최대 극단값 분포
- Minitab이 데이터에 −1을 곱합니다.
- Minitab이 최소 극단값 분포에 대한 공차 구간 절차를 사용하여 변환된 데이터에 대한 공차 구간을 계산합니다.
- Minitab이 이전 단계에서 얻은 공차 구간의 한계를 거듭제곱하여 구간을 원래 데이터의 척도로 변환합니다.
최소 극단값 분포에 적용되는 공식에 대한 내용은 최소 극단값 분포에 대한 항목에서 확인하십시오.
로지스틱 분포
Minitab에서는 Bain과 Engelhardt1 을 기반으로 근사치(1 − α, P) 공차 구간을 계산하며, 여기서 1 − α 은 신뢰 수준이고 P는 적용 범위(구간 내 모집단의 목표 최소 백분율)입니다. 공차 하한 계수의 공식은 공차 하한 계수의 공식과 다릅니다.
단측 로지스틱 공차 한계
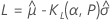
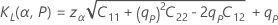
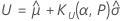
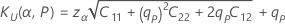
양측 로지스틱 공차 한계
이 분석은 Bonferroni의 부등식2를 갖는 로지스틱 분포에 대한 근사 양측 공차 구간을 생성합니다. 이 근사 방법은 단측 공차 한계를 계산하기 위한 공식에서 α 를 α/2로, P를 ( P + 1)/2로 대체합니다.
표기법
| 용어 | 설명 |
|---|---|
 | 낮은 공차 계수 |
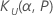 | 상위 공차 계수 |
| zα | 표준 정규 분포의 상위 α 백분위수로, 하위 1 −α 백분위수 점에 해당합니다. |
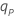 | log(p) − log(1 − p), p× 표준 로지 스틱 분포의 백분위수 100 하한수 |
| C11 |  |
| C22 |  |
| C12 | 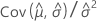 |
 | 로지스틱 위치 모수의 최대우도 추정치 |
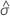 | 로지스틱 척도 모수의 최대우도 추정치 |
- Bain, L. and Englehardt, M. (1991). Statistical analysis of reliability and life testing models: Theory and methods. Second edition, Marcel Dekker, Inc.
- Hahn, G. J. and Meeker, W. Q. (2017). Statistical intervals: A guide for practitioners. Second edition, John Wiley and Sons, Inc.
로그 로지스틱 분포
- Minitab이 데이터의 자연 로그를 취합니다.
- Minitab이 로지스틱 분포에 대한 공차 구간 절차를 사용하여 변환된 데이터에 대한 공차 구간을 계산합니다.
- Minitab이 이전 단계에서 얻은 공차 구간의 한계를 거듭제곱하여 구간을 원래 데이터의 척도로 변환합니다.
로지스틱 분포에 적용되는 공식에 대한 내용은 로지스틱 분포에 대한 항목에서 확인하십시오.
Anderson-Darling 검정
Minitab에서는 적합도 검정을 수행하기 위해 Anderson-Darling 통계량을 사용합니다.
Z = F(X)로 설정합니다. 여기서 F(X)는 누적분포함수입니다. 표본 X1, .., Xn이 Z(i) = F(Xi), i=1,.., n 값을 제공한다고 가정합니다. Z(i)를 오름차순, Z(1) < Z(2) <...<Z(n)으로 재배열합니다. 그런 다음 Anderson-Darling 통계량(A2)은 다음과 같이 계산됩니다.
- A2 = –n - (1/n) Σi[(2i – 1) log Z(i) + (2n + 1 – 2i) log (1 – Z(i))]
수정된 Anderson-Darling 적합도 검정 통계량이 각 분포에 대해 계산됩니다. p-값은 D'Agostino and Stephens의 표에 제공됩니다.1 표에 정확한 p-값이 없는 경우 Minitab에서는 p-값의 범위를 사용한 보간을 기반으로 p-값을 계산합니다.
