공차 구간 방법
Minitab에서는 모수 및 비모수 공차 구간을 모두 계산합니다. 모수 공차 구간 계산에서는 표본의 상위 분포가 정규 분포를 따른다고 가정합니다. 비모수 공차 구간 계산에서는 상위 분포가 계량형이라는 것만 가정합니다.
일반 정의
X 1, X 2, ..., X n을 계량형 분포에서 추출한 크기 n의 랜덤 표본을 기반으로 한 순서 통계량이라고 정의합니다.
분포 함수를 크기가 1보다 크거나 같은 모수 공간에서 Ω에 대한 F(x;θ)로 정의합니다.
L < U를 α 및 P(0 < α < 1, 0 < P < 1) 값이 지정된 경우, Ω의 모든 θ에 대해 다음 조건을 충족하는 표본을 기반으로 하는 두 통계량으로 정의합니다.
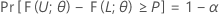
그런 다음, 구간 [ L, U]은 내용 = P x 100%이고 신뢰 수준 = 100(1 - α)%인 양측 공차 구간입니다. 이러한 구간을 양측 (1 - α, P) 공차 구간이라고 합니다. 예를 들어, α = 0.10이고 P = 0.85인 경우 생성되는 구간을 양측 (90%, 0.85) 공차 구간이라고 합니다.
L = –∞이고 U < +∞인 경우 구간 (-∞, U]을 단측 (1 – α, P) 공차 상한이라고 합니다. L > -∞이고 U = +∞인 경우 구간 [L, +∞)을 단측 (1 – α, P) 공차 하한이라고 합니다.
- 단측 (1 – α, P) 공차 하한은 또한 단측 (α, 1 – P) 공차 상한입니다.
- 데이터 분포의 (1 – P)번째 백분위수의 단측 (1 – α )100% 신뢰 하한은 또한 단측 (1 – α, P) 공차 하한입니다. 마찬가지로, 데이터 분포의 P번째 백분위수의 단측 (1 – α )100% 신뢰 상한은 또한 (1 – α , P) 공차 상한입니다.
- L과 U가 단측 (1 – α/2 , (1 + P )/2) 공차 하한 및 상한인 경우 [ L, U ]는 대략적인 양측 (1 – α, P ) 공차 구간입니다. 이 방법은 양측 공차 구간을 직접 얻을 수 없는 경우 사용할 수 있습니다. 그 결과 일반적으로 보수적인 양측 공차 구간이 생성됩니다. Guenther1 및 Hahn and Meeker2를 참조하십시오.
- Guenther, W. C. (1972). Tolerance intervals for univariate distributions. Naval Research Logistics, 19: 309–333.
- Hahn G. J. and Meeker W. Q. (1991). Statistical Intervals: A Guide for Practitioners John Wiley & Sons, New York.
정규 분포에 대한 정확한 공차 구간

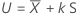
단측 구간에 대한 공차 요인
단측 구간에 대한 정확한 공차 구간은 다음 방정식으로 계산됩니다.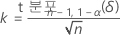
여기서 tn-1,1-α(δ)는 자유도가 n – 1이고 비중심 모수가 δ(다음 공식으로 계산됨)인 비중심 t-분포의 1 – α 백분위수입니다.

양측 구간에 대한 공차 요인
양측 구간에 대한 정확한 공차 요인은 다음 방정식에서 k를 풀어 얻습니다. Krishnamoorthy and Mathew1를 참조하십시오.
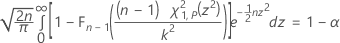
여기서 Fn – 1은 자유도가 n – 1인 카이-제곱 분포의 누적분포함수이고, χ21,p는 자유도가 1이고 비중심 모수가 z2인 비중심 카이-제곱 분포의 P번째 백분위수입니다. 방정식의 왼쪽 부분은 다음과 같이 다시 작성됩니다.
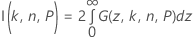
설명:
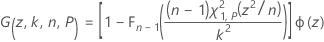
여기서 Φ(z)는 표준 정규 분포의 확률밀도함수입니다. Minitab에서는 36-점 Gauss-Legendre 구적법을 사용하여 I(k, n, P)를 평가합니다.
표기법
| 용어 | 설명 |
|---|---|
| 1 - α | 공차 구간의 신뢰 수준 |
| P | 공차 구간의 범위(구간 내 모집단의 목표 최소 백분율) |
| L | 공차 구간의 하한 |
| U | 공차 구간의 상한 |
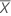 | 표본의 평균 |
| k | 공차 요인(k-요인이라고도 함) |
| S | 표본의 표준 편차 |
| n | 표본의 관측치 수 |
| ZP | 표준 정규 분포의 P번째 백분위수 |
- Krishnamoorthy, K. and Mathew, T. (2009). Statistical Tolerance Regions: Theory, Applications, and Computation. Wiley, Hoboken, NJ.
계량형 분포에 대한 정확한 비모수 공차 구간
Minitab에서는 정확한 (1 – α, P) 비모수 공차 구간을 계산하며, 여기서 1 – α은 신뢰 수준이고 P는 범위(구간 내 모집단의 목표 최소 백분율)입니다. 공차 구간에 대한 비모수 방법은 분포를 사용하지 않는 방법입니다. 즉, 비모수 공차 구간은 표본의 상위 모집단에 종속되지 않습니다. Minitab에서는 단측과 양측 구간 모두에 대해 정확한 방법을 사용합니다.
X 1, X 2 , ... , X n 을 계량형 분포를 따르는 모집단 F(x;θ)에서 추출한 랜덤 표본의 순서 통계량이라고 설정합니다. 그런 다음, Wilks1, 2 및 Robbins3의 결과를 기반으로 다음과 같이 표시할 수 있습니다.

여기서・B는 모수가・a・=・r・및・b・=・n・–・s・+・1인・베타・분포의・누적분포함수를・나타냅니다.・따라서・(・Xr・・,・Xs・)는・구간・범위에・상위・모집단,・F(x;θ)의・분포와・독립적인,・모수・값을・알고・있는・베타・분포가・포함되기・때문에・분포와・관계・없는・공차・구간입니다.・
단측 구간
k를 다음 조건을 만족하는 가장 큰 정수라고 설정합니다.

여기서 Y는 모수가 n 및 1 – P인 이항 랜덤 변수입니다. 단측 (1 – α, P) 공차 하한이 Xk 로 지정될 수 있습니다(Krishnamoorthy and Mathew4 참조). 마찬가지로, 단측 (1 – α, P) 공차 상한은 X n - k +1로 지정됩니다. 두 경우 모두 실제 또는 유효 범위는 P(Y > k)로 지정됩니다.
양측 구간
k를 다음 조건을 만족하는 가장 작은 정수라고 설정합니다.

여기서 V는 모수가 n 및 P인 이항 랜덤 변수입니다. 따라서 다음과 같습니다.
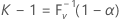
여기서 F V -1(x)는 V의 역 누적분포함수입니다. 양측 (1 – α, P) 공차 구간이 ( Xr , Xs )로 지정될 수 있습니다(Krishnamoorthy and Mathew4 참조). Minitab에서는 r = (n – k + 1) / 2인 s = n - r + 1를 선택합니다. r와 s는 가장 가까운 정수로 내림됩니다. 실제 또는 유효 범위는 P(V < k – 1)로 정의됩니다.
표기법
| 용어 | 설명 |
|---|---|
| 1 – α | 공차 구간의 신뢰 수준 |
| P | 공차 구간의 범위(구간 내 모집단의 목표 최소 백분율) |
| n | 표본의 관측치 수 |
- Wilks, S. S. (1941). Sample size for tolerance limits on a normal distribution. The Annals of Mathematical Statistics, 12, 91–96.
- Wilks, S. S. (1941). Statistical prediction with special reference to the problem of tolerance limits. The Annals of Mathematical Statistics, 13, 400–409.
- Robbins, H. (1944). On distribution-free tolerance limits in random sampling. The Annals of Mathematical Statistics, 15, 214–216.
- Krishnamoorthy, K. and Mathew, T. (2009). Statistical Tolerance Regions: Theory, Applications, and Computation. Wiley, Hoboken, NJ.
