이 항목의 내용
분포 매개변수의 최대 우도 추정치
최대 우도 방법은 각 분포에 대한 우도 함수를 최대화하는 분포 모수의 값을 추정하기 위해 사용됩니다. 목표는 분포 모형과 관측된 표본 데이터 사이에 최적의 "합치도"를 얻는 것입니다.
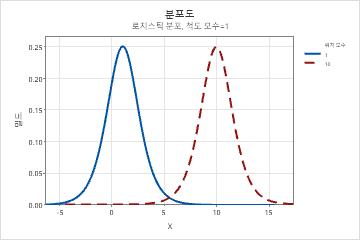
- 위치
- 이 모수는 분포 위치에 영향을 미칩니다. 예를 들어, 여러 위치 모수를 사용하면 로지스틱 분포가 수평 축을 따라 이동할 수 있습니다.
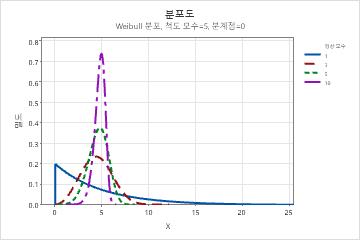
- 형상
- 이 모수는 분포 형상에 영향을 미칩니다. 예를 들어, 여러 형상 모수를 사용하면 Weibull 분포가 더 치우치거나 더 대칭적으로 보일
수 있습니다.
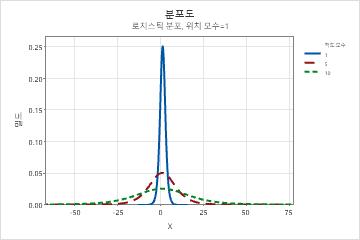
- 척도
- 이 모수는 분포 척도에 영향을 미칩니다. 예를 들어, 여러 척도 모수를 사용하면 로지스틱 분포가 더 "확장"되거나 더 압축된 것으로 보일
수 있습니다.
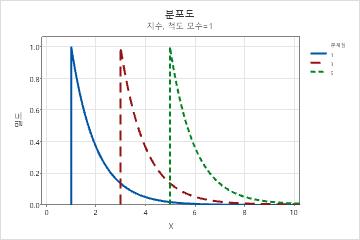
- 분계점
- 이 모수는 랜덤 변수의 최소값에 영향을 미칩니다. 예를 들어, 여러 분계점 모수를 사용하면 다른 값의 범위에서 지수 분포를 정의할 수
있습니다.
참고
Minitab에서는 불편화 모수 추정치를 사용하는 정규 분포와 대수 정규 분포를 제외한 모든 분포에 대해 최대우도 방법을 사용하여 모수 추정치를 계산합니다.
해석
데이터에 사용되는 특정 분포 모형을 이해하려면 분포 모수의 최대우도 추정치를 사용하십시오. 예를 들어, 한 품질 엔지니어가 과거의 공정 지식과 Anderson-Darling 및 LRT p-값을 기반으로 3-모수 Weibull 분포가 공정 데이터에 대해 최량 적합치를 제공하는 것을 확인한다고 가정합니다. 데이터 모델링에 사용되는 특정 3-모수 Weibull 분포를 이해하기 위해 엔지니어는 분포에 대해 계산된 모양, 크기 및 임계값에 대한 최대 우도 추정치를 조사합니다.
분포
개별 분포 식별은 일반적으로 사용되는 여러 분포에 대한 적합도 통계량과 분포 모수를 제공합니다. 이 중 대부분의 분포가 유용하며 양수 값, 음수 값, 0이 포함된 데이터 등 여러 계량형 데이터를 모형화할 수 있습니다.
- 2-모수 대수 정규 분포
- 1-모수 지수 분포
- 2-모수 Weibull 분포
- 2-모수 감마 분포
- 2-모수 로그 로지스틱 분포
따라서 데이터에 음수 값이나 0이 포함된 경우 Minitab에서는 이러한 특정 분포에 대한 결과를 보고하지 않습니다. 이 경우 각 분포의 더 높은 모수 버전에 대한 결과를 사용하십시오. 예를 들어, 데이터에 음수 값이 포함된 경우 Minitab에서는 2-모수 대수 정규 분포에 대한 결과를 보고하지 않습니다. 대신 3-모수 대수 정규 분포에 대한 결과를 사용하십시오.
개별 분포 식별에 사용되는 분포에 대한 자세한 내용은 Weibull 분포가 비정규 공정 능력 분석의 기본 분포인 이유에서 확인하십시오.
참고
각 분포에 대한 PDF와 CDF를 계산하기 위해 사용되는 공식에 대한 내용은 개별 분포 식별의 분포에 대한 방법 및 공식에서 확인하십시오.
