In This Topic
Regression equation
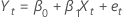
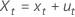
In orthogonal regression, the best fitting line is the one that minimizes the weighted orthogonal distances from the plotted points to the line. If the error variance ratio is 1, the weighted distances are Euclidean distances.
Notation
| Term | Description |
|---|---|
| Yt | observed response |
| β0 | intercept |
| β1 | slope |
| Xt | observed predictor |
| xt | true and unobserved value of predictor |
| et, ut | measurement errors; et, ut are independent with mean 0 and error variances of δe2 and δu2 |
Sample covariance matrix
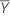 ,
, 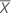 ) and the sample covariance matrix be:
) and the sample covariance matrix be:
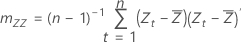

Notation
| Term | Description |
|---|---|
| Zt | (Yt, Xt) |
 |  |
| n | sample size |
Error variances
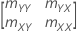
If the element mXY of the sample covariance matrix does not equal 0, then:
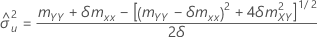
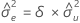
If mXY = 0 and mYY < δmXX,

Notation
| Term | Description |
|---|---|
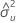 | estimate of error variance for X |
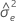 | estimate of error variance for Y |
| δ | ratio of error variances |
| mXY | element of sample covariance matrix |
| mYY | element of sample covariance matrix |
| mXX | element of sample covariance matrix |
Coefficients

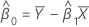
If mxy = 0 and myy < δm xx','

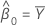
If mxy = 0 and myy > δmxx, the remaining parameter estimates are undefined.
Notation
| Term | Description |
|---|---|
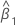 | estimate of slope |
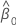 | estimate of intercept |
| mxy | element of sample covariance matrix |
| myy | element of sample covariance matrix |
| δ | ratio of error variances |
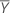 | mean of response values |
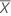 | mean of predictor values |
Covariance matrix of approximate distribution
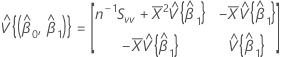
where:
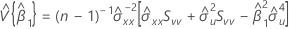
and
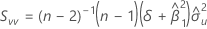
If mXY does not equal 0:
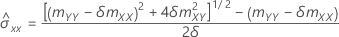
If mXY equals 0 and mYY < δmXX:
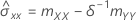
Notation
| Term | Description |
|---|---|
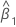 | estimate of slope |
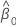 | estimate of intercept |
| mXY | element of sample covariance matrix |
| mYY | element of sample covariance matrix |
| mXX | element of sample covariance matrix |
| δ | ratio of error variances |
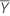 | mean of response values |
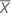 | mean of predictor values |
Confidence interval for intercept
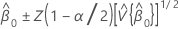
Z (1 - α / 2) is the 100 * (1 - α / 2 ) percentile for the standard normal distribution
and
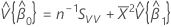 , which is an element in the covariance matrix of the approximate distribution
, which is an element in the covariance matrix of the approximate distribution Notation
| Term | Description |
|---|---|
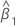 | estimate of slope |
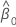 | estimate of intercept |
| α | level of significance |
Confidence interval for slope
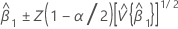
where:
Z(1 - α / 2) is the 100 * (1 - α / 2) percentile for the standard normal distribution
and
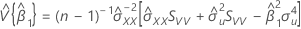
Notation
| Term | Description |
|---|---|
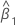 | estimate of slope |
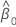 | estimate of intercept |
| α | level of significance |
Fitted values for x
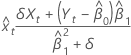
Notation
| Term | Description |
|---|---|
| δ | ratio of error variances |
| Yt | tth response value |
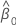 | intercept estimate |
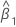 | slope estimate |
Fitted values for y
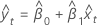
Notation
| Term | Description |
|---|---|
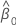 | intercept estimate |
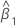 | slope estimate |
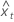 | tth fitted value for x |
Residuals
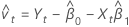
Notation
| Term | Description |
|---|---|
| Yt | tth response value |
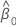 | intercept |
| Xt | tth predictor value |
 | slope |
Standardized residuals

where

Notation
| Term | Description |
|---|---|
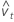 | residual |
 | standard deviation of residual |
| δ | error variance ratio |
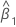 | estimate of slope |
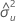 | estimate of error variance for X |
Predictor of Y
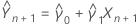
where:
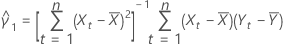
and
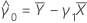
Notation
| Term | Description |
|---|---|
| Xt | tth predictor value |
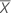 | mean of predictor values |
| Yt | tth response value |
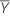 | mean of response values |
Standard deviation for the prediction error

where:
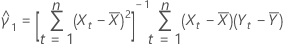
Notation
| Term | Description |
|---|---|
| myy | sample variance of Y |
| mxy | sample covariance between X and Y random variables |
