In This Topic
Coefficients
Two methods to find the maximum likelihood estimates of the coefficients exist. One method is to maximize directly the likelihood function with respect to the coefficients. These expressions are nonlinear in the coefficients. The alternative method is to use an iterative reweighted least squares (IRWLS) approach, which is the method that Minitab uses to obtain the estimates of the coefficients. McCullagh and Nelder1 show that the two methods are equivalent. However, the iterative reweighted least squares method is easier to implement. For details, see 1.
One-step approximation method for some cases of k-fold cross-validation
For some large-sample designs with many cross-validation folds, Minitab uses a one-step approximation method in the cross-validation algorithm to decrease the calculation time (see Pregibon2 and Williams3). For these designs, rather than fit the training model for a fold with the IRWLS algorithm to full convergence, the cross-validation statistics for the fold come from the regression parameters from the first iterative step of the algorithm.
The following table shows which designs get cross-validation statistics from the 1-step approximation.
| Sample size (n) | Number of columns in the design matrix (p) | Number of folds (k) |
|---|---|---|
| 200 < n ≤ 500 | 150 < p ≤ 300 | k > 200 |
| p > 300 | k > 100 | |
| 500 < n ≤ 1000 | 100 < p ≤ 300 | k > 300 |
| p > 300 | k > 150 | |
| 1000 < n ≤ 10,000 | p ≤ 50 | k > 1,000 |
| 50 < p ≤ 200 | k > 200 | |
| 200 < p ≤ 400 | k > 50 | |
| p > 400 | k > 10 | |
| 10,000 < n ≤ 50,000 | p ≤ 50 | k > 200 |
| 50 < p ≤ 200 | k > 100 | |
| p > 200 | k > 20 | |
| 50,000 < n ≤ 100,000 | p ≤ 50 | k > 100 |
| 50 < p ≤ 150 | k > 50 | |
| p > 150 | k > 20 | |
| n > 100,000 | Any value of p | k > 100 |
One-step approximation algorithm
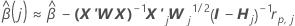
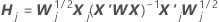
Notation
| Term | Description |
|---|---|
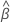 | the estimated coefficients fit with the full data set |
| X | the design matrix for the full data set |
| X' | the transverse of the design matrix for the full data set |
| W | the weight matrix for the full data set |
| X'j | the design matrix for the data in the jth fold |
| Wj | the weight matrix for the data in the jth fold |
| I | the identity matrix |
| rp, j | the vector of Pearson residuals from the model for the full data set for the data in the jth fold |
[1] P. McCullagh and J. A. Nelder (1989). Generalized Linear Models, 2nd Ed., Chapman & Hall/CRC, London.
[2] D. Pregibon (1981). Logistic regression diagnostics. The Annals of Statistics, 9(4), 705-724.
[3] D. A. Williams (1987). Generalized linear model diagnostics using the deviance and single case deletions, Applied Statistics, 36(2), 181-191.
Standard error of coefficients
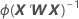
W is a diagonal matrix where the diagonal elements are given by the following formula:
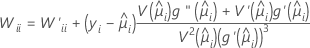
where

This variance-covariance matrix is based on the observed Hessian matrix as opposed to the Fisher's information matrix. Minitab uses the observed Hessian matrix because the model that results is more robust against any conditional mean misspecification.
If the canonical link is used then the observed Hessian matrix and the Fisher's information matrix are identical.
Notation
| Term | Description |
|---|---|
| yi | the response value for the ith row |
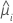 | the estimated mean response for the ith row |
| V(·) | the variance function given in the table below |
| g(·) | the link function |
| V '(·) | the first derivative of the variance function |
| g'(·) | the first derivative of the link function |
| g''(·) | the second derivative of the link function |
The variance function depends on the model:
| Model | Variance function |
| Binomial | 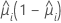 |
| Poisson | 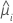 |
See [1] and [2] for more information.
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh and J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Z
The Z-statistic used to determine whether the predictor is significantly related to the response. Larger absolute values of Z indicate a significant relationship. The formula is:
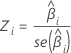
Notation
| Term | Description |
|---|---|
| Zi | The test statistic for a standard normal distribution |
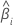 | The estimated coefficient |
 | The standard error of the estimated coefficient |
For small samples, the likelihood-ratio test may be a more reliable test of significance. The likelihood ratio p-values are in the deviance table. When the sample size is large enough, the p-values for the Z statistics approximate the p-values for the likelihood ratio statistics.
p-value (P)
Used in hypothesis tests to help you decide whether to reject or fail to reject a null hypothesis. The p-value is the probability of obtaining a test statistic that is at least as extreme as the actual calculated value, if the null hypothesis is true. A commonly used cut-off value for the p-value is 0.05. For example, if the calculated p-value of a test statistic is less than 0.05, you reject the null hypothesis.
Odds ratios for binary logistic regression
The odds ratio is provided only if you select the logit link function for a model with a binary response. In this case, the odds ratio is useful in interpreting the relationship between a predictor and a response.
The odds ratio (τ) can be any nonnegative number. The odds ratio = 1 serves as the baseline for comparison. If τ = 1, no association exists between the response and predictor. If τ < 1, the odds of the event are higher for the reference level of the factor (or for lower levels of a continuous predictor). If τ > 1, the odds of the event are less for the reference level of the factor (or for lower levels of a continuous predictor). Values farther from 1 represent stronger degrees of association.
Note
For the binary logistic regression model with one covariate or factor, the estimated odds of success are:
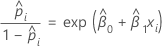
The exponential relationship provides an interpretation for β: The odds increase multiplicatively by eβ1 for every one-unit increase in x. The odds ratio is equivalent to exp(β1).
For example, if β is 0.75, the odds ratio is exp(0.75), which is 2.11. This indicates that there is a 111% increase in the odds of success for every one unit increase in x.
Notation
| Term | Description |
|---|---|
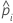 | the estimated probability of a success for the ith row in the data |
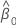 | the estimated intercept coefficient |
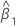 | the estimated coefficient for predictor x |
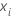 | the data point for the ith row |
Confidence interval
The large sample confidence interval for an estimated coefficient is:
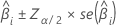
For binary logistic regression, Minitab provides confidence intervals for the odds ratios. To obtain the confidence interval of the odds ratio, exponentiate the lower and upper limits of the confidence interval. The interval provides the range in which the odds may fall for every unit change in the predictor.
Notation
| Term | Description |
|---|---|
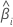 | the ith coefficient |
 | the inverse cumulative probability of the standard normal distribution at 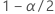 |
 | the significance level |
 | the standard error of the estimated coefficient |
Variance-covariance matrix
A d x d matrix, where d is the number of predictors plus one. The variance of each coefficient is in the diagonal cell and the covariance of each pair of coefficients is in the appropriate off-diagonal cell. The variance is the standard error of the coefficient squared.
The variance-covariance matrix is from the final iteration of the inverse of the information matrix. The variance-covariance matrix has the following form:
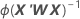
W is a diagonal matrix where the diagonal elements are given by the following formula:

where

This variance-covariance matrix is based on the observed Hessian matrix as opposed to the Fisher's information matrix. Minitab uses the observed Hessian matrix because the model that results is more robust against any conditional mean misspecification.
If the canonical link is used then the observed Hessian matrix and the Fisher's information matrix are identical.
Notation
| Term | Description |
|---|---|
| yi | the response value for the ith row |
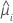 | the estimated mean response for the ith row |
| V(·) | the variance function given in the table below |
| g(·) | the link function |
| V '(·) | the first derivative of the variance function |
| g'(·) | the first derivative of the link function |
| g''(·) | the second derivative of the link function |
The variance function depends on the model:
| Model | Variance function |
| Binomial | 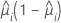 |
| Poisson | 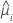 |
See [1] and [2] for more information.
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh and J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
