Select the method or formula of your choice.
In This Topic
Notation
The notation is critical to understanding ANOVA models. Listed below is the notation used for one-way analysis of variance.
| Term | Description |
|---|---|
| r | number of levels of the factor, i = 1 ...r |
| i | a given factor level |
| j | a given case for a particular factor level, j = 1 ...n i |
| yij | j th observation of the response for the i th factor level |
| ni | number of observations for the i th factor level |
| n T | total number of cases |
| μi | true mean of observations at the i th factor level |
| yi. | total of the observations at the i th factor level |
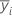 | mean of the response for the ith factor |
Model fitting
Formula
The one-way analysis of variance model can be specified in several ways. The cell means model is:
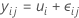
All observations for the factor level have the same expectation, μ i . Because μi is a constant, all observations have the same variance, regardless of factor level.
In analysis of variance, least squares estimation is used to fit the model and provide estimates for the parameters, μi .
The hypothesis test for one-way analysis of variance is:
H0: μ 1 = μ 2= … = μ r
H1: At least one mean is not equal to the others
Notation
| Term | Description |
|---|---|
| μ i | parameters or the true mean of observations at the i th factor level |
| ε ij | error that is independently and normally distributed with mean 0 and constant variance σ 2 |
