Select the method or formula of your choice.
In This Topic
Parameter constraints
Enforce parameter constraints by transforming the parameters.1
| If | Then |
|---|---|
| a < θ | θ = a + exp( φ ) |
| θ < b | θ = b - exp( φ ) |
| a < θ < b | θ = a +((b - a) / (1 + exp( -φ ))) |
| Term | Description |
|---|---|
| a and b | numeric constants |
| θ's | parameters |
| φ | transformed parameters |
Minitab performs these transforms, and displays the results in terms of the original parameters.
- Bates and Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.
Standard error of the parameter estimate
The approximate standard error of the estimate of θp is S times the square root of diagonal element p of 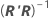 , which is written as:
, which is written as:

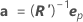

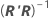 , which is written as:
, which is written as:

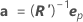

Notation
| Term | Description |
|---|---|
| n | nth observation |
| N | total number of observations |
| p | number of free (unlocked) parameters |
| R | the (upper triangular) R matrix from the QR decomposition of Vi for the final iteration |
| V0 | gradient matrix = ( ∂f(xn, θ) / ∂θp), the P by 1 vector of partial derivatives of f(x0, θ), evaluated at θ* |
| S |
 |
Correlation matrix of the parameter estimates
The approximate variance-covariance matrix of the parameter estimates is:
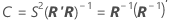
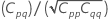

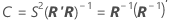
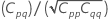

Notation
| Term | Description |
|---|---|
| R | the (upper triangular) R matrix from the QR decomposition of Vi for the final iteration |
| P | number of free (unlocked) parameters |
| v0 | gradient matrix = ( ∂f(xn, θ) / ∂θ p), the P by 1 vector of partial derivatives of f( x0, θ), evaluated at θ* |
| θ's | parameters |
Profile likelihood confidence intervals for parameters
Let θ = (θ1, . . . . θp) * with θ* being the final iteration for θ.
The likelihood-based 100 (1 - α) % confidence limits satisfy:
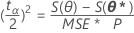
where S( θp ) is the SSE obtained when holding θp fixed and minimizing over the other parameters.1 This is equivalent to solving:
S(θp) = S(θ*) + (tα/2)2 MSE
Notation
| Term | Description |
|---|---|
| θ's | parameters |
| n | nth observation |
| N | total number of observations |
| P | number of free (unlocked) parameters |
| tα/2 | upper α/2 point of the t distribution with N - P degrees of freedom |
| S(θ) | Sum of the squared error |
| MSE | mean squared error |
- Bates and Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.
