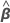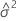In This Topic
The mixed effects model and the log-likelihood
The general form of the mixed effects model
Mixed effects models contain both fixed and random effects. The general form of the mixed effects model is:
y = Xβ + Z1μ1 + Z2μ2 + ... + Zcμc + ε
Notation
| Term | Description |
|---|---|
| y | the n x 1 vector of response values |
| X | the n x p design matrix for the fixed effect terms, p ≤ n |
| β | a p x 1 vector of unknown parameters |
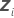 | the n x mi design matrix for the 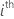 random term in the model random term in the model |
| μi | an mi x 1 vector of independent variables from N(0,  ) ) |
| ε | an n x 1 vector of independent variables from N(0,  ) ) |
| n | the number of observations |
| p | the number of parameters in  |
| c | the number of random terms in the model |
Variance-covariance matrix
Based on the model assumption for the general form of the mixed effects model, the response vector, y, has a multivariate normal distribution with mean vector Xβ and the following variance-covariance matrix:
V(σ2) = V(σ2, σ21, ... , σ2c) = σ2In + σ21Z1Z'1 + ... + σ2cZcZ'c
where
σ2 = (σ2, σ21, ... , σ2c)'
σ2, σ21, ... , σ2c are called variance components.
By factoring from the variance, you can find a representation of H(θ), which is in the computation of the log-likelihood of mixed effects models.
V(σ2) = σ2H(θ) = σ2[In + θ1Z1Z'1 + ... + θcZcZ'c]
Notation
| Term | Description |
|---|---|
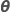 | 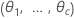 |
| θi | 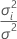 , the ratio of the variance of the , the ratio of the variance of the 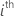 random term over the error variance random term over the error variance |
Log-likelihood


Notation
| Term | Description |
|---|---|
| H | In + θ1Z1Z'1 + ... + θcZcZ'c |
| |H| | the determinant of H |
| H-1 | the inverse of H |
| mi | the number of levels for the 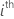 random term random term |
 | the error variance component |
| In | the identity matrix with n rows and columns |
Restricted Maximum Likelihood (REML) estimation
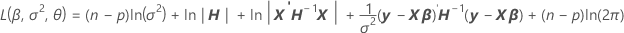
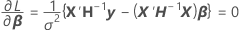
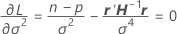
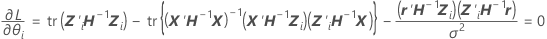
where 
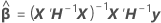
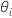 cannot be explicitly solved for the
cannot be explicitly solved for the 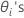 . Minitab uses Newton's method to estimate
. Minitab uses Newton's method to estimate 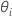 with the following steps:
with the following steps:
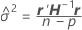
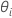 are the variance ratio estimates. The variance component for the
are the variance ratio estimates. The variance component for the 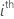 random term is as follows:
random term is as follows:

Notation
| Term | Description |
|---|---|
| tr(·) | the trace of the matrix |
| X' | the transpose of X |