The central limit theorem is a fundamental theorem of probability and statistics. The theorem describes the distribution of the mean of a random sample from a population with finite variance. When the sample size is sufficiently large, the distribution of the means is approximately normally distributed. The theorem applies regardless of the shape of the population's distribution. Many common statistical procedures require data to be approximately normal. The central limit theorem lets you apply these useful procedures to populations that are strongly nonnormal. How large the sample size must be depends on the shape of the original distribution. If the population's distribution is symmetric, a sample size of 5 could yield a good approximation. If the population's distribution is strongly asymmetric, a larger sample size is necessary. For example, the distribution of the mean might be approximately normal if the sample size is greater than 50. The following graphs show examples of how the distribution affects the sample size that you need.
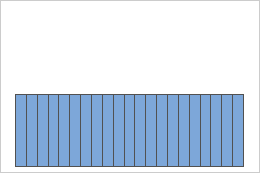
Uniform distribution
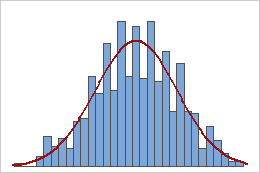
Sample means
Samples from a uniform population
A population that follows a uniform distribution is symmetric but strongly nonnormal, as the first histogram demonstrates. However, the distribution of sample means from 1000 samples of size 5 from this population is approximately normal because of the central limit theorem, as the second histogram demonstrates. This histogram of sample means includes a superimposed normal curve to illustrate its normality.
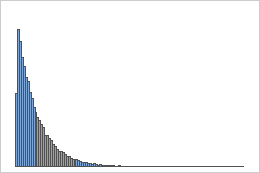
Exponential distribution
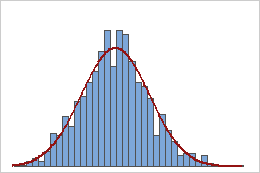
Sample means
Samples from an exponential population
A population that follows an exponential distribution is asymmetric and nonnormal, as the first histogram demonstrates. However, the distribution of sample means from 1000 samples of size 50 from this population is approximately normal because of the central limit theorem, as the second histogram demonstrates. This histogram of sample means includes a superimposed normal curve to illustrate its normality.
