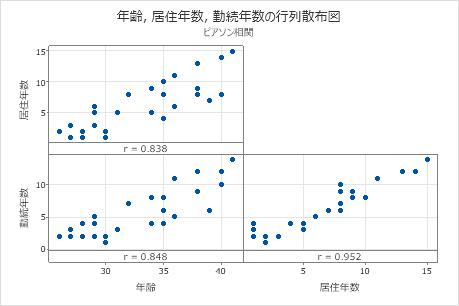
ピアソン相関
相関行列は、変数の各ペアの間の線形関係を測定する相関値を示します。相関値は-1~+1の範囲になります。2つの変数が一緒に増減する傾向にあるとき、相関値は正になります。1つの変数が増加したとき他方の変数が減少する場合には、相関値は負になります。
解釈
相関行列を使用して、2つの変数間の関係の強さと方向を評価します。正の相関値が高い場合、変数が同じ特徴を測定していることを示しています。項目の相関が高くない場合、項目はそれぞれ異なる特徴を示すこともあれば、関係がはっきりしないこともあります。
相関
| 年齢 | 居住年数 | 勤続年数 | 貯蓄 | 借金 | |
|---|---|---|---|---|---|
| 居住年数 | 0.838 | ||||
| 勤続年数 | 0.848 | 0.952 | |||
| 貯蓄 | 0.552 | 0.570 | 0.539 | ||
| 借金 | 0.032 | 0.186 | 0.247 | -0.393 | |
| クレジットカード数 | -0.130 | 0.053 | 0.023 | -0.410 | 0.474 |
- 住所と年齢、0.838
- 雇用状況と年齢、0.848
- 雇用状況と住所、0.952
- 負債と貯蓄、−0.393
- クレジットカードと年齢、−0.130
- クレジットカードと貯蓄、−0.410
スピアマン相関
スピアマン相関係数を使用して、2つの連続変数または順位変数の間の単調関係の強さと方向を調べます。単調関係では、変数が同じ相関方向に動く傾向がありますが、一定の割合とは限りません。スピアマン相関を計算するために、Minitabでは生データが順位付けされます。続いて、順位付けされたデータの相関係数が計算されます。
- 強度
-
相関係数の範囲は-1~+1の値です。係数の絶対値が大きいほど、変数間の関係は強まります。
スピアマンの相関では、絶対値が1の場合、順位データが完全に線形であることを示します。たとえば、スピアマンの相関が−1の場合、変数Aの最高値が変数Bの最低値に関連付けられ、変数Aの2番目に高い値が変数Bの2番目に低い値に関連付けられ、という関係になっていることを意味します。
- 方向
-
相関係数の符号は関係の方向を示します。2つの変数がともに増加または減少する場合、係数は正で、相関を表す線の傾きが右上がりになります。一方の変数が増加するともう一方が減少する傾向にある場合、係数は負になり、相関を表す線の傾きが右下がりになります。
以下のプロットは、変数間の関係の強さと方向のさまざまなパターンを図示するために、特定のスピアマン相関係数値のあるデータを示しています。

関係なし: スピアマンのρ = 0
点はプロット上にランダムに落ちており、変数間に関係がないことを示しています。
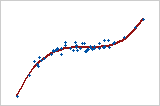
強い正の関係: スピアマンのρ = 0.948
点は線に近く、変数間に強い関係があることを示しています。変数が共に増大しているため、関係は正です。

強い負の関係: スピアマンのρ = -1.0
点は線に近く、変数間に強い関係があることを示しています。1つの変数が増加したとき他方の変数が減少するため、関係は負です。
相関関係のみに基づいて、ある変数の変化が別の変数変化の原因となると結論付けることは決して適切ではありません。関係における因果関係の有無は、適切に制御された実験でのみ決定されます。
解釈
相関
| 年齢 | 居住年数 | 勤続年数 | 貯蓄 | 借金 | |
|---|---|---|---|---|---|
| 居住年数 | 0.824 | ||||
| 勤続年数 | 0.830 | 0.912 | |||
| 貯蓄 | 0.570 | 0.571 | 0.496 | ||
| 借金 | -0.198 | -0.142 | -0.056 | -0.605 | |
| クレジットカード数 | -0.179 | 0.069 | 0.036 | -0.480 | 0.353 |
ペアワイズのスピアマン相関
| サンプル1 | サンプル2 | N | 相関 | ρの95%信頼区間 | p値 |
|---|---|---|---|---|---|
| 居住年数 | 年齢 | 30 | 0.824 | (0.624, 0.922) | 0.000 |
| 勤続年数 | 年齢 | 30 | 0.830 | (0.636, 0.926) | 0.000 |
| 貯蓄 | 年齢 | 30 | 0.570 | (0.236, 0.783) | 0.001 |
| 借金 | 年齢 | 30 | -0.198 | (-0.524, 0.178) | 0.293 |
| クレジットカード数 | 年齢 | 30 | -0.179 | (-0.508, 0.197) | 0.345 |
| 勤続年数 | 居住年数 | 30 | 0.912 | (0.798, 0.963) | 0.000 |
| 貯蓄 | 居住年数 | 30 | 0.571 | (0.237, 0.784) | 0.001 |
| 借金 | 居住年数 | 30 | -0.142 | (-0.479, 0.232) | 0.454 |
| クレジットカード数 | 居住年数 | 30 | 0.069 | (-0.300, 0.419) | 0.719 |
| 貯蓄 | 勤続年数 | 30 | 0.496 | (0.144, 0.737) | 0.005 |
| 借金 | 勤続年数 | 30 | -0.056 | (-0.408, 0.311) | 0.768 |
| クレジットカード数 | 勤続年数 | 30 | 0.036 | (-0.328, 0.392) | 0.849 |
| 借金 | 貯蓄 | 30 | -0.605 | (-0.804, -0.283) | 0.000 |
| クレジットカード数 | 貯蓄 | 30 | -0.480 | (-0.726, -0.124) | 0.007 |
| クレジットカード数 | 借金 | 30 | 0.353 | (-0.020, 0.639) | 0.056 |
これらの結果では、住所と年齢の間のスピアマン相関は0.824で、変数間に正の関係があることを示しています。ρの信頼区間は0.624~0.922です。p値は0.000で、関係がα = 0.05レベルで統計的に有意であることを示しています。
負債と貯蓄の間のスピアマン相関は-0.605、クレジットカードと貯蓄の間のスピアマン相関は-0.480です。これらの変数間の関係は負で、負債とクレジットカードが増えると貯蓄が減ることを示しています。
使用した行
使用した行数が方法表に表示されます。これは欠損値を含むデータの行数です。
欠損値がある時、使用した行数は信頼区間の計算で使用した実際のサンプルサイズと同じではありません。
相関の信頼区間
信頼区間は、相関係数の値が含まれる可能性が高い範囲です。データのサンプルはランダムであるため、2つの母集団サンプルの信頼区間が同一である可能性は低くなります。しかし、サンプルを何度も繰り返して測定すると、得られた信頼区間または限界値の特定の割合に未知の相関係数が含まれることになります。このような相関係数を含む信頼区間や限界値の割合(%)を区間の信頼水準と言います。
たとえば、95%の信頼水準は、母集団から100個のサンプルをランダムに採取した場合、そのうちおよそ95個からは相関係数を含む区間が得られると期待することができます。
上限は、母集団差がそれより小さくなる可能性が高い値です。下限は、母集団差がそれより大きくなる可能性が高い値です。
ピアソン相関の信頼区間は、基になる二変量分布の正規性に対して敏感です。データが正規性から逸脱した場合、信頼区間は、サンプルサイズの大きさにかかわらず、正確ではないかもしれません。
スピアマン相関の信頼区間は順位に基づき、基になる二変量分布の仮説に対してそれほど敏感ではありません。
解釈
信頼区間により、結果の実質的な有意性を評価しやすくなります。状況に応じた専門知識を利用して、信頼区間に実質的に有意な値が含まれているかどうかを判断します。信頼区間が広すぎて役に立たない場合、サンプルサイズを増加させることを検討します。 詳細は信頼区間の精度を高める方法を参照してください。
ペアワイズのピアソン相関
| サンプル1 | サンプル2 | N | 相関 | ρの95%信頼区間 | p値 |
|---|---|---|---|---|---|
| 居住年数 | 年齢 | 30 | 0.838 | (0.684, 0.920) | 0.000 |
| 勤続年数 | 年齢 | 30 | 0.848 | (0.702, 0.926) | 0.000 |
| 貯蓄 | 年齢 | 30 | 0.552 | (0.240, 0.761) | 0.002 |
| 借金 | 年齢 | 30 | 0.032 | (-0.332, 0.388) | 0.865 |
| クレジットカード数 | 年齢 | 30 | -0.130 | (-0.468, 0.242) | 0.494 |
| 勤続年数 | 居住年数 | 30 | 0.952 | (0.901, 0.977) | 0.000 |
| 貯蓄 | 居住年数 | 30 | 0.570 | (0.264, 0.772) | 0.001 |
| 借金 | 居住年数 | 30 | 0.186 | (-0.187, 0.512) | 0.326 |
| クレジットカード数 | 居住年数 | 30 | 0.053 | (-0.313, 0.406) | 0.779 |
| 貯蓄 | 勤続年数 | 30 | 0.539 | (0.222, 0.753) | 0.002 |
| 借金 | 勤続年数 | 30 | 0.247 | (-0.125, 0.557) | 0.189 |
| クレジットカード数 | 勤続年数 | 30 | 0.023 | (-0.340, 0.380) | 0.906 |
| 借金 | 貯蓄 | 30 | -0.393 | (-0.660, -0.038) | 0.032 |
| クレジットカード数 | 貯蓄 | 30 | -0.410 | (-0.671, -0.059) | 0.024 |
| クレジットカード数 | 借金 | 30 | 0.474 | (0.138, 0.713) | 0.008 |
この結果では、住所および年齢に、正の線形相関0.838があります。95%の信頼度で、母相関係数は0.684~0.920と考えることができます。通常、相関が強いと、信頼区間が狭くなります。例えば、クレジットカードと年齢の相関は弱く、95%信頼区間は-0.468~0.242です。
p値
p値は帰無仮説を棄却するための証拠を測定する確率です。p値が小さいほど、帰無仮説を棄却するための強力な証拠となります。
解釈
相関係数が統計的に有意かどうかを判断するにはp値を使用します。
- p値 ≤ α: 相関は統計的に有意です(H0を棄却する)
- p値が有意水準以下の場合は、帰無仮説を棄却する決定を下します。相関が統計的に有意であると結論付けることができます。専門知識に基づいて、差が実際に有意かどうかを判断します。詳細は、統計的有意性と実質的有意性を参照してください。
- p値 > α: 相関は統計的に有意ではありません(H0を棄却しない)
- p値が有意水準よりも大きい場合は、帰無仮説を棄却しない決定を下します。相関が統計的に有意であると結論付けるのに十分な証拠がありません。
ピアソン相関法とスピアマン相関法の両方のp値手順は正規性から離れるデータに対して頑健です。p値は通常、サンプルの親母集団に関係なく、n ≥ 25に対して正確です。
ペアワイズのピアソン相関
| サンプル1 | サンプル2 | N | 相関 | ρの95%信頼区間 | p値 |
|---|---|---|---|---|---|
| 居住年数 | 年齢 | 30 | 0.838 | (0.684, 0.920) | 0.000 |
| 勤続年数 | 年齢 | 30 | 0.848 | (0.702, 0.926) | 0.000 |
| 貯蓄 | 年齢 | 30 | 0.552 | (0.240, 0.761) | 0.002 |
| 借金 | 年齢 | 30 | 0.032 | (-0.332, 0.388) | 0.865 |
| クレジットカード数 | 年齢 | 30 | -0.130 | (-0.468, 0.242) | 0.494 |
| 勤続年数 | 居住年数 | 30 | 0.952 | (0.901, 0.977) | 0.000 |
| 貯蓄 | 居住年数 | 30 | 0.570 | (0.264, 0.772) | 0.001 |
| 借金 | 居住年数 | 30 | 0.186 | (-0.187, 0.512) | 0.326 |
| クレジットカード数 | 居住年数 | 30 | 0.053 | (-0.313, 0.406) | 0.779 |
| 貯蓄 | 勤続年数 | 30 | 0.539 | (0.222, 0.753) | 0.002 |
| 借金 | 勤続年数 | 30 | 0.247 | (-0.125, 0.557) | 0.189 |
| クレジットカード数 | 勤続年数 | 30 | 0.023 | (-0.340, 0.380) | 0.906 |
| 借金 | 貯蓄 | 30 | -0.393 | (-0.660, -0.038) | 0.032 |
| クレジットカード数 | 貯蓄 | 30 | -0.410 | (-0.671, -0.059) | 0.024 |
| クレジットカード数 | 借金 | 30 | 0.474 | (0.138, 0.713) | 0.008 |
これらの結果には、有意水準0.05未満のp値が多くあり、ピアソン相関係数が統計的に有意であることを示しています。
注
極端なデータ点が原因でp値が小さいものの、信頼区間は非常に広い、というケースがあります。例えば、クレジットカードと負債では、95% CIは非常に広いですが、p値は小さいです。行列プロットを調べると、極端なデータ点を見ることができます。
行列散布図
行列散布図は、散布図を並べたものです。行列の各散布は、x軸とy軸上の項のペアのスコアをグラフ化したものです。
解釈
プロットを使用して、変数のすべての組み合わせにおける関係を視覚的に評価します。関係は線形、単調関係であるか、またはどちらにも当てはまらないかもしれません。また、行列プロットを使用して、結果に大きな影響を与え得る外れ値を探します。関係の種類に関する詳細は、線形、非線形、および単調関係を参照してください。
この行列プロットは、すべての項目ペアに正の線形関係があることを示します。