帰無仮説と対立仮説
- 帰無仮説
- 帰無仮説では母集団パラメータ(平均や標準偏差など)は仮説値に等しいと仮定します。帰無仮説とは多くの場合、前回の分析や専門知識を基にした最初の主張を指します。
- 対立仮説
- 対立仮説では、母集団パラメータは帰無仮説の仮説値よりも小さい、大きい、異なると仮定します。対立仮説とは、真であると確信できる、または真であることの証明が期待できる仮説を指します。
出力では、帰無仮説と対立仮説により、仮説平均として正しい値を入力したことを検証できます。
N
サンプルサイズ(N)は、サンプルに含まれる観測値の合計数です。
解釈
サンプルサイズは、信頼区間と検定の検出力に影響します。
通常、サンプルサイズが大きいほど信頼区間が狭くなります。また、サンプルサイズが大きいほど、検定での差の検出力が高くなります。詳細は、検出力とはを参照してください。
平均
平均とは、すべてのサンプル値を1つの値で要約したもので、データの中心を表します。平均値は、データの平均であり、すべての観測値の和を観測値の数で割って求められる値です。
解釈
サンプルデータの平均は、母平均の推定値です。
平均は母集団全体ではなくサンプルデータに基づくため、サンプル平均が母平均に一致する可能性は低いと言えます。より良好に母平均を推定するためには、信頼区間を使用します。
標準偏差
標準偏差とは、散布度、つまり平均を中心としたデータの広がり方を表す最も一般的な測度です。記号σ(シグマ)は、母集団の標準偏差を示す場合によく使用されますが、sはサンプルの標準偏差を示す場合にも使用されます。多くの場合、工程に対してランダム(自然)な変動は雑音と呼ばれます。
標準偏差は、データと同じ単位を使用します。
解釈
標準偏差を使用して、平均からのデータの拡散程度を判断します。 標準偏差の値が高いほど、データの広がりが大きいことを示します。 正規分布の経験則によれば、値のおよそ68%が平均の1つの標準偏差の範囲内にあり、値の95%が2つの標準偏差の範囲内にあり、値の99.7%が3つの標準偏差の範囲内にあります。
サンプルデータの標準偏差は、母集団標準偏差の推定値です。 標準偏差は、信頼区間とp値を計算するために使用します。 値を大きくすると、より精度の低い(広い)信頼区間と、検出力が低い検定が生成されます。
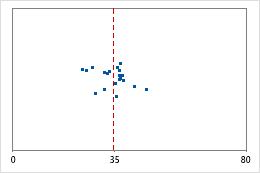
病院1

病院2
退院時間
管理者が、2つの病院の救急部門で処置を受けた患者の退院時間を追跡するとします。平均退院時間はほぼ同じ(35分)ですが、標準偏差には有意差があります。病院1の標準偏差はおよそ6です。平均すると、患者の退院時間は平均(点線)から約6分離れています。病院2の標準偏差はおよそ20です。平均すると、患者の退院時間は平均(点線)から約20分離れることになります。
平均の標準誤差
平均の標準誤差(平均のSE)では、同じ母集団から繰り返しサンプルを抽出した場合に得られるサンプル平均間の変動性が推定されます。平均の標準誤差はサンプル間の変動性を推定し、標準偏差は単一サンプル内の変動性を測定します。
たとえば、ランダムサンプルである312個の配達時間に基づいた平均配達時間は3.80日、標準偏差は1.43日であるとします。この数値から求められる平均の標準誤差は、0.08日(1.43を312の平方根で割ったもの)です。同じ母集団から同じサイズのランダムサンプルを複数抽出すると、異なるサンプル平均の標準偏差はおよそ0.08日になります。
解釈
平均の標準誤差を使用して、サンプル平均がどれだけ正確に母集団平均を推定するかを判断します。
平均の標準誤差の値が小さいと、母平均の推定値の精度が高くなります。通常、標準偏差が大きいと、平均の標準誤差が大きくなり、母平均の推定値の精度が低くなります。サンプルサイズが大きいと、平均の標準誤差が小さくなり、母平均の推定値の精度が高くなります。
Minitabは、平均の標準誤差を使用して信頼区間を計算します。
信頼区間(CI)と限界
信頼区間は、母平均の値が含まれる可能性が高い範囲です。データのサンプルはランダムであるため、2つの母集団サンプルの信頼区間が同一である可能性は低くなります。しかし、サンプルを何度も繰り返して測定すると、得られた信頼区間または限界値の特定の割合に未知の母平均が含まれることになります。このような平均を含む信頼区間や限界値の割合(%)を区間の信頼水準と言います。たとえば、95%の信頼水準は、母集団から100個のサンプルをランダムに採取した場合、そのうちおよそ95個からは母平均を含む区間が得られると期待することができます。
上限は、母平均がそれより小さくなる可能性が高い値です。下限は、母平均がそれより大きくなる可能性が高い値です。
信頼区間により、結果の実質的な有意性を評価しやすくなります。状況に応じた専門知識を利用して、信頼区間に実質的に有意な値が含まれているかどうかを判断します。信頼区間が広すぎて役に立たない場合、サンプルのサイズを増加させることを検討します。 詳細は、信頼区間の精度を高める方法を参照してください。
記述統計量
| N | 平均 | 標準偏差 | 平均の標準誤差 | μに対する95%信頼区間 |
|---|---|---|---|---|
| 25 | 330.6 | 154.2 | 30.8 | (266.9, 394.2) |
これらの結果では、エネルギーコストの推定母平均は330.6です。95%の信頼度で、母平均は266.9から394.2の間に含まれると考えることができます。
t値
t値とは、標準誤差の単位で観測サンプル統計量とその仮説母集団パラメータの差を測定するt検定統計量の観測値です。
解釈
t値をt分布の棄却限界値と比較して、帰無仮説を棄却するかどうかを判断できます。ただし通常は、検定のp値を使用して同じ決定を下すほうがより実用的で便利です。
帰無仮説を棄却するかどうかを判断するには、t値を棄却限界値と比較します。棄却限界値は、両側検定の場合はtα/2, n–1、片側検定の場合はtα, n–1です。両側検定においては、t値の絶対値が棄却限界値よりも大きい場合、帰無仮説を棄却します。Z値の絶対値が棄却値より大きい場合、帰無仮説を棄却します。Minitabで棄却限界値を計算することも、ほとんどの統計に関する書籍に掲載されているt分布表で棄却限界値を見つけることもできます。詳細は、逆累積分布関数(ICDF)の使用に進み、「逆累積分布関数で棄却限界値を計算する」をクリックします。
p値
p値は帰無仮説を棄却するための証拠を測定する確率です。p値が小さいほど、帰無仮説を棄却するための強力な証拠となります。
解釈
p値を使用して、母平均が仮説平均と統計的に異なるかどうかを判断します。
- p値 ≤ α: 平均値の間の差は統計的に有意です(H0を棄却する)
- p値が有意水準以下の場合は、帰無仮説を棄却する決定を下します。母平均と仮説平均の差は統計的に有意であると結論付けることができます。専門知識に基づいて、差が実際に有意かどうかを判断します。詳細は、統計的有意性と実質的有意性を参照してください。
- p値 > α: 平均値の間の差は統計的に有意ではありません(H0を棄却しない)
- p値が有意水準よりも大きい場合は、帰無仮説を棄却しない決定を下します。母平均と仮説平均の差は統計的に有意であると結論付けるだけの十分な証拠はありません。検定の検出力が、実質的に有意な差を検出するのに十分であることを確認してください。詳細は、1サンプルtの検出力とサンプルサイズを参照してください。
ヒストグラム
ヒストグラムは、サンプル値を多数の区間に分割し、各区間内のデータ値の度数をバーで表します。
解釈
ヒストグラムを使用してデータの形状と広がりを評価します。 ヒストグラムは、サンプルサイズが20より大きい場合に最適です。
- 歪んだデータ
-
データの広がりを調べて、データが歪んでいるかどうかを判断します。データが歪んでいる場合、大半のデータがグラフの上側または下側に表示されます。多くの場合、ヒストグラムまたは箱ひげ図で最も簡単に歪度を検出できます。
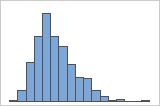
右方向の歪み
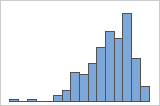
左方向の歪み
データが右方向に歪んだヒストグラムは、待ち時間を示しています。ほとんどの待ち時間は比較的短く、いくつかの待ち時間のみが長くなっています。データが左方向に歪んだヒストグラムは、故障時間データを示しています。一部の項目はすぐに故障していますが、多くの項目は故障するまでに長い時間がかかっています。
サンプルが小さい(値が20個未満の)場合、大きく歪んだデータはp値の妥当性に影響する可能性があります。データが大きく歪んでいてサンプルが小さい場合は、サンプルサイズを大きくすることを検討してください。
- 外れ値
-
他のデータ値から遠く離れている外れ値は、分析結果に大きく影響する可能性があります。多くの場合、箱ひげ図で最も簡単に外れ値を識別できます。

ヒストグラムでは、グラフのどちらかの端にある孤立したバーで潜在的な外れ値が示されます。
外れ値の原因を特定する必要があります。データ入力や測定の誤差を修正します。異常な1回きりの事象(特別原因)のデータ値は除外することを検討します。その後で、分析を繰り返します。詳細は、外れ値の識別を参照してください。
個別値プロット
個別値プロットには、サンプルの個別値が表示されます。各円は1つの観測値を表しています。個別値プロットは、観測値数が比較的少なく、各観測値の効果も評価する必要がある場合に特に便利です。
解釈
個別値プロットを使用して、データの広がりを調べ、潜在的な外れ値を識別します。 個別値プロットは、サンプルサイズが50未満の場合に最適です。
- 歪んだデータ
-
データの広がりを調べて、データが歪んでいるかどうかを判断します。データが歪んでいる場合、大半のデータがグラフの上側または下側に表示されます。多くの場合、ヒストグラムまたは箱ひげ図で最も簡単に歪度を検出できます。
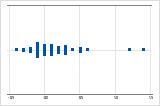
右方向の歪み
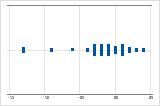
左方向の歪み
データが右方向に歪んだ個別値プロットは、待ち時間を示しています。ほとんどの待ち時間は比較的短く、いくつかの待ち時間のみが長くなっています。データが左方向に歪んだ個別値プロットは、故障時間データを示しています。一部の項目はすぐに故障していますが、多くの項目は故障するまでに長い時間がかかっています。
サンプルが小さい(値が20個未満の)場合、大きく歪んだデータはp値の妥当性に影響する可能性があります。データが大きく歪んでいてサンプルが小さい場合は、サンプルサイズを大きくすることを検討してください。
- 外れ値
-
他のデータ値から遠く離れている外れ値は、分析結果に大きく影響する可能性があります。多くの場合、箱ひげ図で最も簡単に外れ値を識別できます。
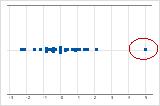
個別値プロットでは、異常に低いか高いデータ値で潜在的な外れ値が示されます。
外れ値の原因を特定する必要があります。データ入力や測定の誤差を修正します。異常な1回きりの事象(特別原因)のデータ値は除外することを検討します。その後で、分析を繰り返します。詳細は、外れ値の識別を参照してください。
箱ひげ図
箱ひげ図は、サンプルの分布を視覚的に要約します。データの形状、中心傾向、および変動性が表示されます。
解釈
箱ひげ図を使用して、データの広がりを調べ、潜在的な外れ値を識別します。 箱ひげ図は、サンプルサイズが20より大きい場合に最適です。
- 歪んだデータ
-
データの広がりを調べて、データが歪んでいるかどうかを判断します。データが歪んでいる場合、大半のデータがグラフの上側または下側に表示されます。多くの場合、ヒストグラムまたは箱ひげ図で最も簡単に歪度を検出できます。

右方向の歪み

左方向の歪み
データが右方向に歪んだ箱ひげ図は、待ち時間を示しています。ほとんどの待ち時間は比較的短く、いくつかの待ち時間のみが長くなっています。データが左方向に歪んだ箱ひげ図は、故障時間データを示しています。一部の項目はすぐに故障していますが、多くの項目は故障するまでに長い時間がかかっています。
サンプルが小さい(値が20個未満の)場合、大きく歪んだデータはp値の妥当性に影響する可能性があります。データが大きく歪んでいてサンプルが小さい場合は、サンプルサイズを大きくすることを検討してください。
- 外れ値
-
他のデータ値から遠く離れている外れ値は、分析結果に大きく影響する可能性があります。多くの場合、箱ひげ図で最も簡単に外れ値を識別できます。
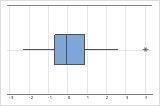
箱ひげ図では、アスタリスク(*)で外れ値が示されます。
外れ値の原因を特定する必要があります。データ入力や測定の誤差を修正します。異常な1回きりの事象(特別原因)のデータ値は除外することを検討します。その後で、分析を繰り返します。詳細は、外れ値の識別を参照してください。
