このトピックの内容
ステップ1:各制御因子の最適な水準を特定する
SN比を使用して、雑音因子に起因する変動性を最小化する制御因子設定を特定します。Minitabでは制御因子の各組み合わせに対してSN比が計算され、その後各制御因子の水準それぞれに対して平均SN比が計算されます。実験の目的に応じ、期待される結果を理解したうえで、4つのSN比から適切なものを選択します。詳細はタグチ計画のSN比とはを参照してください。
デルタとは、各因子の最大平均応答と最小平均応答との差です。順位はデルタ値に基づいて、最大のデルタ値が順位1、次に大きいデルタ値が順位2、という風に割り当てられ、応答に対する各因子の相対的な効果が表されます。
SN比の応答表
| 水準 | 品種 | 光 | 肥料 | 水 | 噴霧頻度 |
|---|---|---|---|---|---|
| 1 | -1.9266 | -0.6911 | -4.1399 | -0.9870 | 0.2274 |
| 2 | 2.8068 | 1.5712 | 5.0201 | 1.8672 | 0.6527 |
| デルタ | 4.7333 | 2.2623 | 9.1600 | 2.8542 | 0.4253 |
| 順位 | 2 | 4 | 1 | 3 | 5 |
傾きの応答表
| 水準 | 品種 | 光 | 肥料 | 水 | 噴霧頻度 |
|---|---|---|---|---|---|
| 1 | 0.6867 | 0.6043 | 0.5264 | 0.5437 | 0.7067 |
| 2 | 0.7440 | 0.8264 | 0.9043 | 0.8870 | 0.7240 |
| デルタ | 0.0572 | 0.2220 | 0.3778 | 0.3433 | 0.0174 |
| 順位 | 4 | 3 | 1 | 2 | 5 |
標準偏差の応答表
| 水準 | 品種 | 光 | 肥料 | 水 | 噴霧頻度 |
|---|---|---|---|---|---|
| 1 | 0.7794 | 0.5450 | 0.7677 | 0.5222 | 0.6207 |
| 2 | 0.5042 | 0.7387 | 0.5159 | 0.7614 | 0.6629 |
| デルタ | 0.2752 | 0.1937 | 0.2518 | 0.2392 | 0.0422 |
| 順位 | 1 | 4 | 2 | 3 | 5 |
主要な結果:デルタ、順位
- 肥料(デルタ値9.1600、順位1)がSN比に対して最も大きい影響力を持ち、次に品種(デルタ値4.7333、順位2)、水量、光量、噴霧頻度と続きます。
- 肥料(デルタ値0.3778、順位1)は傾きに対しても最も大きい影響力を持ち、次に水量(デルタ値0.3433、順位2)、光量、品種、噴霧頻度と続きます。
- 品種(デルタ値0.2752、順位1)が標準偏差に対して最も大きい影響力を持ち、次に肥料(デルタ値0.2518、順位2)、水量、光量、噴霧頻度と続きます。
注
静的計画で信号因子がない場合は、傾きの代わりに平均の応答表が表示されます。
ステップ2:応答に対して統計的に有意な効果を持つ因子を特定する
- p値 ≤ α:関連性は統計的に有意である
- p値が有意水準以下の場合は、応答変数と項の間に統計的に有意な関連性が存在すると結論付けることができます。
- p値 > α:その関連性は統計的に有意ではない
- p値が有意水準より大きい場合は、応答変数と項の間に統計的に有意な関連性があると結論することはできません。項を持たないモデルを再適合したいと考えるかもしれません。
- 因子の係数が有意な場合は、すべての水準平均が等しいとは限らないと結論付けることができます。
- 交互作用項の係数が有意な場合は、因子と応答の間の関係はその項の他の因子に依存します。こうしたケースでは、交互作用の影響の考慮なしに主効果を解釈すべきではありません。
モデル項が統計的に有意でない場合、モデル項を削除してモデルを再適合することができます。通常、有意水準0.10はモデル内の項の評価に使用されます。
係数は、モデル内の項と応答変数の関係の大きさと方向を表します。係数の絶対値は、各因子の相対強度を示します。因子に対して計算される係数の数は、水準数から1を引いた数です。因子に3つの水準がある場合、2つの係数が用意され、因子水準1と2に対応します。因子に2つの水準がある場合、1つの係数が用意され、因子水準1に対応します。水準に対応する値またはテキストも用意されます。
応答表には、各因子のそれぞれの水準の応答特性の平均値が表示されています。また、効果の相対的な大きさを比較するために、デルタ統計量による順位も表示されています。デルタ統計量とは、各因子の最大平均から最小平均を引いたものです。順位はデルタ値に基づいて割り当てられ、最大のデルタ値が順位1、次に大きいデルタ値が順位2、という順になります。応答表の水準平均値を使用して、各因子のどの水準が最適な結果を提供するか判定します。
SN比に対する推定モデル係数
| 項 | 係数 | 係数の標準誤差 | T値 | p値 |
|---|---|---|---|---|
| 定数 | 0.4401 | 0.2384 | 1.846 | 0.316 |
| 品種 1 | -2.3667 | 0.2384 | -9.926 | 0.064 |
| 光 1 | -1.1312 | 0.2384 | -4.744 | 0.132 |
| 肥料 1 | -4.5800 | 0.2384 | -19.209 | 0.033 |
| 水 1 | -1.4271 | 0.2384 | -5.985 | 0.105 |
| 噴霧頻度 1 | -0.2127 | 0.2384 | -0.892 | 0.536 |
| 品種*肥料 1 1 | -0.6041 | 0.2384 | -2.534 | 0.239 |
モデル要約
| S | R二乗 | R二乗 (調整済み) |
|---|---|---|
| 0.6744 | 99.81% | 98.69% |
SN比の分散分析
| 要因 | 自由度 | 逐次平方和 | 調整平方和 | 調整平均平方 | F値 | p値 |
|---|---|---|---|---|---|---|
| 品種 | 1 | 44.809 | 44.809 | 44.809 | 98.52 | 0.064 |
| 光 | 1 | 10.236 | 10.236 | 10.236 | 22.51 | 0.132 |
| 肥料 | 1 | 167.811 | 167.811 | 167.811 | 368.97 | 0.033 |
| 水 | 1 | 16.293 | 16.293 | 16.293 | 35.82 | 0.105 |
| 噴霧頻度 | 1 | 0.362 | 0.362 | 0.362 | 0.80 | 0.536 |
| 品種*肥料 | 1 | 2.920 | 2.920 | 2.920 | 6.42 | 0.239 |
| 残差誤差 | 1 | 0.455 | 0.455 | 0.455 | ||
| 合計 | 7 | 242.886 |
主要な結果:p値、係数
この例で、SN比においては肥料のp値は0.05より小さいため、肥料は有意水準0.05において統計的に有意です。
ステップ3:因子の効果を図表を用いて調べる
注
効果を表示させるためにこれらのプロットを利用することはできますが、モデルに適合する分析における効果の統計的有意性も必ず評価してください。交互作用の効果が分析において統計的に有意な場合は、主効果の解釈では必ず交互作用効果も考慮する必要があります。
主効果プロット
主効果プロットでは、各因子がいかに応答特性(SN比、平均、傾き、標準偏差)に影響を与えるかが示されます。主効果は、因子の異なる水準が特性に異なる影響を与える場合に存在します。2つの水準を持つ因子の場合、一方の水準の方がもう一方の水準よりも平均を高める場合があります。この違いが主効果になります。
- この線が水平方向である場合は、主効果が存在しません。因子の各水準は特性に対して一様に影響を与えます。また、特性平均値はすべての因子水準について同じです。
- この線が水平方向ではない場合は、主効果が存在します。因子の水準が異なると、特性に与える影響も異なります。プロットされたデータ点の垂直位置の差が大きいほど(線とX軸が平行でなくなるほど)、主効果も大きくなります。
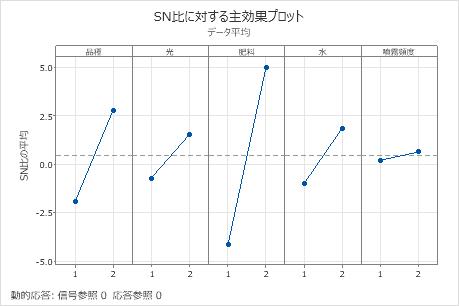
この結果でSN比の主効果プロットは、肥料がSN比に対して最も大きい影響力を持つことを示しています。平均して、肥料2を使った実験のSN比の方が肥料1を使った実験よりもはるかに高くなっています。噴霧頻度では、S/N比の効果が小さいか効果がありません。
交互作用プロット
- これらの直線が互いに平行な場合、2つの因子の間に交互作用はありません。
- これらの直線が互いに平行でない場合、2つの因子の間には交互作用があります。
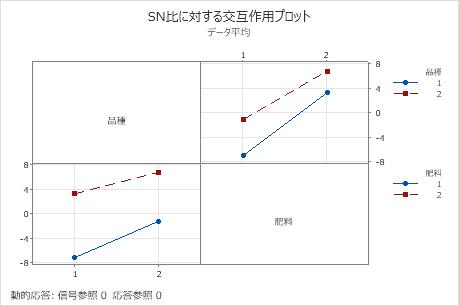
この結果で、SN比においては線はほぼ平行になっています。肥料1と2のどちらを使用しても、品種2のほうが品種1よりもSN比が高くなっています。
交互作用プロットに加え、線形モデル分析も調べて交互作用が有意かどうかを判断します。
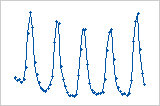
散布図
- 参照点を通る最小二乗回帰直線。
- そのプロットの因子設定が最初に現れる行を表す、各プロットの先頭の行番号。
- プロットの底部に表示される、因子設定のSN比、傾き、および標準偏差。
これらのグラフは、比が最大となる実験の実行が最初にプロットされるよう、SN比の降順に配列されています。実験における因子設定の組み合わせが10以上の場合、散布図のグラフが複数表示されます。
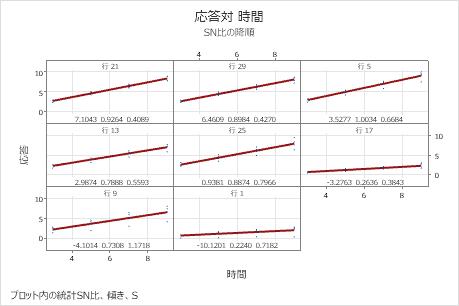
このプロットでは、最良の適合と最悪の適合との間に、データのばらつきの実質的な差が見られます。たとえば、第1セルのプロットでは、行21のデータは回帰直線に非常に近く位置しています。左下隅のセルでは、行9のデータははるかに大きな広がりを見せています。行21の標準偏差は0.4089ですが、行9の標準偏差は1.1718と、非常に大きくなっています。
ステップ4:モデルが分析の仮説を満たすかどうか判断する
残差プロットを使用して、モデルが適切か、分析の仮定が満たされているかどうかを判断しやすくします。仮定を満たさない場合、そのモデルはデータにあまり適合しない可能性があり、結果の解釈は慎重に行う必要があります。
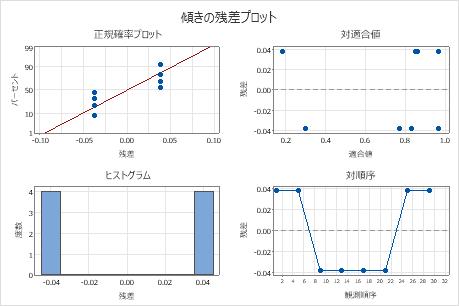
これらの結果の残差プロットには、誤差に対して自由度は1つのみで、別個の残差値は2つのみであることが示されています。項の数が多すぎて、モデルが過剰に適合している可能性が高いです。このような場合、モデルを縮小して再度残差プロットを調査してみてください。
残差の正規確率プロット
残差の正規確率プロットを使用して、残差が正規分布に従うという仮定を検証します。残差の正規確率プロットは、ほぼ直線になります。
以下の表にあるパターンは、このモデルが、モデルの仮説を満たさないことを示している可能性があります。
| パターン | パターンが示す意味 |
|---|---|
| 直線ではない | 非正規性 |
| 直線から離れた点 | 外れ値 |
| 傾きが変化する | 未確認の変数 |
残差対適合値プロット
以下の表にあるパターンは、このモデルが、モデルの仮説を満たさないことを示している可能性があります。| パターン | パターンが示す意味 |
|---|---|
| 残差が適合値周辺に扇状または不均等に分散している | 不均一分散 |
| 曲線 | 高次の項の欠損 |
| ゼロから遠い点 | 外れ値 |
| ある点が他の点からX軸方向に遠く離れている | 影響力のある点 |
残差対適合値プロットを使用して、残差はランダムに分布し、均一な分散が存在するという仮定を検証します。点が特徴的なパターン無く0の両側にランダムに来るのが理想的です。
残差のヒストグラム
| パターン | パターンが示す意味 |
|---|---|
| 1つの方向に伸びている | 歪度 |
| 1本のバーが他のバーから離れている | 外れ値 |
ヒストグラムの外観は、データをグループ化するために使用されている区間の数に依存するので、残差の正規性を評価するときにヒストグラムは使用しません。
ヒストグラムは、観測値が約20個以上ある場合に最も効果的です。サンプルが小さすぎる場合、ヒストグラム上の各バーには歪度や外れ値を確実に表示するだけの十分な観測値がありません。
残差対順序プロット
トレンド
シフト