効果
効果は項と応答変数の関係の大きさと方向を表します。Minitabでは、因子の効果と因子間の交互作用が計算されます。
解釈
効果のサイズはリンク関数の変化に対応します。Logitリンク関数を使用する場合、効果のサイズは因子の低水準から高水準までの変化の対数オッズ比です。効果の符号は項と応答変数の関係の方向を表します。
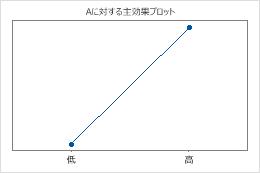
交互作用の因子が多いほど、効果の解釈が難しくなります。因子および因子間の交互作用において、効果の大きさは、応答変数に対して項が持つ影響力の実質的な有意性を評価するのに役立ちます。
効果の大きさは、項の統計的な有意性は示しません。これは有意性の計算には応答データの変動も考慮されるためです。統計的な有意性を判断するには、項のp値を調べます。
係数
回帰係数は、予測変数と応答変数の関係の、サイズと方向を表します。係数とは、回帰式において項の値に乗じられる数です。
解釈
予測変数の変化により事象が発生する可能性が高くなるか低くなるかを特定するには係数を使います。項の係数は、他の項は一定に保たれている中で1つのコード化単位の増加に関連するリンク関数の変化を表しています。
効果の大きさは、応答変数に対して項が持つ影響力の実質的な有意性を評価するのに役立ちます。効果の大きさは、項の統計的な有意性は示しません。これは有意性の計算には応答データの変動も考慮されるためです。統計的な有意性を判断するには、項のp値を調べます。
係数と確率の関係は、リンク関数や応答の参照事象、またモデル内のカテゴリ予測変数の参照水準など、分析におけるいくつかの側面によって異なります。一般的に係数が正数の場合は事象が発生する可能性が高く、負数の場合は低くなります。予測係数が0に近い場合、予測変数の影響が小さいことを表しています。
- 共変量
- 共変量の係数は共変量と同じ単位になります。係数は共変量が1増えた場合のリンク関数の変化を表しています。係数が負数の場合、共変量が増えるに従って確率が下がります。係数が正数の場合、共変量が増えるに従って確率が上がります。共変量はコード化されておらず通常、因子とも直行していないため、共変量があると大抵VIF値は増えます。詳細は、VIFのセクションを参照してください。
- ブロック
- ブロックは(-1, 0, +1)のコード体系を持つカテゴリ変数です。各係数はブロックのリンク関数と平均値の差を表しています。
- 中心点
- 中心点の場合、中心点の項は1としてコード化され、その他の点は0としてコード化されています。中心点の項は、計画に含まれる因子と同じくらいの数の、別名関係にある2次効果を表すので、通常は中心点の項の係数は解釈しません。通常、p値を使用して、因子の2次効果を推定するために追加収集するデータの値を判断します。
logitリンク関数の解釈
Logitリンクは推定係数を最も自然に解釈することができるため、Minitabではデフォルトのリンクとして使用しています。解釈では、参照事象のオッズがP(事象あり)かP(事象なし)であるという事実を使用し、他の予測変数が定数のままであると仮定します。対数オッズが大きくなるほど、参照事象の可能性は高くなります。したがって、係数が正の場合、事象の可能性は高くなり、係数が負の場合、事象の可能性は低くなります。異なるタイプの因子の解釈の要約は以下になります。
- 連続因子
- 連続因子の係数は、因子のコード化単位が1単位ずつ増加したときの参照事象のオッズの自然対数の推定変化です。たとえば、時間因子のコード化単位それぞれが30秒の変化を表し、時間の係数が1.4の場合、オッズの自然対数は、時間を30秒増やすごとに1.4ずつ増加します。
- カテゴリ因子
- 2水準因子の場合、カテゴリ因子の係数は、2つの水準の間にあると解釈されます。カテゴリ因子の係数は、1コード化単位当たりの変化に対する事象のオッズの自然対数の推定変化です。カテゴリ因子の低い水準と高い水準の差は2コード化単位です。たとえば、カテゴリ変数には、「早い」と「遅い」の水準があるとします。「遅い」は下限であり、-1にコード化されます。「早い」は上限であり、+1にコード化されます。変数の係数が1.3の場合、「遅い」から「早い」に変化すると、事象のオッズの自然対数は2.6増加します。
係数の標準誤差
係数の標準誤差により、同じ母集団から繰り返しサンプルを抽出する場合に得られる係数推定値間の変動を推定します。計算では、サンプルを繰り返し抽出する場合はサンプルのサイズと係数の推定値は変わらないと仮定します。
解釈
係数の標準誤差を使用して、係数の推定値の精度を測定します。標準誤差が小さいほど、推定値の精度が高くなります。
係数の信頼区間(95%の信頼区間)
これらの信頼区間(CI)は、モデルにおける各項に対する係数の真の値を含む可能性が高い値の幅です。
データのサンプルはランダムであるため、2つの母集団サンプルの信頼区間が同一である可能性は低くなります。しかし、ランダムなサンプルを何度も繰り返して測定すると、得られた信頼区間の特定の割合に未知の母集団パラメータが含まれることになります。このようなパラメータを含む信頼区間の割合(%)を区間の信頼水準と言います。
- 点推定
- この単一値は、サンプルデータを使用して母数を推定するためのものです。
- 誤差幅
- 誤差幅は、信頼区間の幅を定義し、事象確率、サンプルサイズ、信頼水準の範囲に影響を受けます。
解釈
信頼区間を使用して、モデルの各項の母集団係数の推定値を評価します。
たとえば、信頼水準が95%の場合、信頼区間に母集団の係数の値が含まれていることが95%信頼できます。信頼区間により、結果の実質的な有意性を評価しやすくなります。状況に応じた専門知識を利用して、信頼区間に実質的に有意な値が含まれているかどうかを判断します。信頼区間が広すぎて役に立たない場合、サンプルのサイズを増加させることを検討します。
Z値
Z値は、係数とその標準誤差の比率を測定するワルド検定の検定統計量です。
解釈
MinitabではZ値を使用してp値を計算し、これに基づいて項およびモデルの統計的有意性を判断します。サンプルサイズが十分に大きく、サンプルの係数の分布が正規分布に従う場合、ワルド検定は正確です。
Z値が0から十分に離れている場合は、係数の推定値が、0から統計的に異なるほど十分に大きくかつ正確であることを示しています。逆にZ値が0に近い場合は、係数の推定値が小さすぎる、または精度が低すぎて、項が応答に対して影響を及ぼすとは確信できないことを示しています。
逸脱表で表示される検定は尤度比検定です。係数表の拡張表に表示されるのはワルドの近似検定です。サンプルが小さい場合、尤度比検定のほうがワルドの近似検定よりも正確になります。
p値
p値は帰無仮説を棄却するための証拠を測定する確率です。確率が低いほど、帰無仮説を棄却する強力な証拠となります。
逸脱表で表示される検定は尤度比検定です。係数表の拡張表に表示されるのはワルドの近似検定です。サンプルが小さい場合、尤度比検定のほうがワルドの近似検定よりも正確になります。
解釈
係数が0から統計的に異なるかどうかを判断するには、項のp値と有意水準を比較して帰無仮説を評価します。この帰無仮説は、係数は0に等しく、項と応答に関連性がないという仮定です。
通常は、有意水準(αまたはアルファとも呼ばれる)として0.05が適切です。0.05の有意水準は、実際には係数は0であるにも関わらず、0ではないと結論付けるリスクが5%であることを示しています。
- p値 ≤ α:関連性は統計的に有意である
- p値が有意水準以下の場合は、応答変数と項の間に統計的に有意な関連性が存在すると結論付けることができます。
- p値 > α:その関連性は統計的に有意ではない
- p値が有意水準より大きい場合は、応答変数と項の間に統計的に有意な関連性があると結論することはできません。項を持たないモデルを再適合したいと考えるかもしれません。
- 因子
- 因子の係数が有意な場合は、事象の確率が全ての因子水準で同じではないと結論付けることができます。
- 因子間の交互作用
- 交互作用の係数が統計的に有意な場合は、因子と応答の間の関係がその項の他の因子に依存すると結論付けることができます。
- 共変量
- 共変量の係数が統計的に有意な場合、応答と共変量の関連性は統計的に有意であると結論付けることができます。
- ブロック
- ブロックの係数が統計的に有意な場合、ブロックのリンク関数は平均値と異なると結論付けることができます。
- 中心点
- 中心点の係数が統計的に有意な場合は、少なくとも1つの因子が応答と曲線関係にあると結論付けることができます。曲面性をモデル化するために、計画に軸点を追加してみてください。
logitリンク関数の解釈
Logitリンクは推定係数を最も自然に解釈することができるため、Minitabではデフォルトのリンクとして使用しています。解釈では、参照事象のオッズがP(事象あり)かP(事象なし)であるという事実を使用し、他の予測変数が定数のままであると仮定します。対数オッズが大きくなるほど、参照事象の可能性は高くなります。したがって、係数が正の場合、事象の可能性は高くなり、係数が負の場合、事象の可能性は低くなります。異なるタイプの因子の解釈の要約は以下になります。
- 連続因子
- 連続因子の係数は、因子のコード化単位が1単位ずつ増加したときの参照事象のオッズの自然対数の推定変化です。たとえば、時間因子のコード化単位それぞれが30秒の変化を表し、時間の係数が1.4の場合、オッズの自然対数は、時間を30秒増やすごとに1.4ずつ増加します。
- カテゴリ因子
- 2水準因子では、カテゴリ因子の係数を2つの水準の間で解釈することができます。カテゴリ因子の係数は、コード化単位の変化に対する事象のオッズの自然対数の推定変化になります。カテゴリ因子の低水準と高水準の違いは、2つのコード化単位です。たとえば、カテゴリ変数に、「早い」と「遅い」の水準があるとします。遅いは-1とコード化された低水準です。早いは+1とコード化された高水準です。変数の係数が1.3の場合、「遅い」から「早い」に変化すると、事象のオッズの自然対数は2.6増加します。
VIF
分散拡大要因(VIF: Variance Inflation Factor)は、モデルの予測変数間の相関が、回帰係数の分散をどのくらい増大させるかを示しています。
解釈
モデル内にどれだけ多重共線性(予測変数との相関)が存在するかを示すにはVIFを用います。ほとんどの要因計画でVIF値はすべて1で、これは予測変数に多重共線性がないことを表しています。多重共線性がなければ、統計的有意性の決定は簡単になります。VIF値が大きくなる主な二つの要因は、モデル内に共変量が含まれることと、データ収集時に実行に不備があることで、これにより統計的有意性の決定は複雑化します。2値応答の場合もVIF値はたいてい1よりも大きくなります。
| VIF | 予測変数ステータス |
|---|---|
| VIF = 1 | 相関なし |
| 1 < VIF < 5 | 穏やかに相関 |
| VIF > 5 | 強く相関 |
- 予測変数と応答間に重要な関係が存在するにもかかわらず、係数は統計的に有意でないように見えます。
- 高度に相関する予測変数の係数がサンプル間で大きく異なる。
- モデルから高度に相関する項を除外すると、他の高度に相関する項の推定された係数に大きく影響を及ぼします。高度に相関する項の係数は効果の方向を変えてしまうこともあります。
統計的有意性を使用して、多重共線性のあるモデルから項を削除するときは注意が必要です。モデルから項を1つずつ追加・削除します。モデルを変更するときは、統計的有意性の検定とモデル要約統計量の変化を監視します。
