自由度(DF)
合計自由度(DF)は、データに含まれる情報量のことです。分析では、その情報を使用して、係数の値を推定します。合計自由度DFはデータの行数から1を引いた数です。項の自由度は、その項が使う係数の数を示します。モデルの項の数を増やすと、モデルに係数が追加され、残差誤差の自由度が減少します。誤差の自由度は、モデルでは使用されていない残りの自由度です。
注
2水準要因計画またはプラケット-バーマン計画では、計画に中心点がある場合、1つの自由度は曲面性の検定に使用されます。中心点に対する項がモデルに含まれている場合、曲面性の行はモデルの一部です。中心点に対する項がモデルに含まれていない場合、曲面性の行はモデルに含まれる項を検定するのに使用される誤差の一部です。応答曲面計画および決定的スクリーニング計画では、曲面性の検定が不要になるように、二乗項を推定することができます。
逐次逸脱度
- モデル
- 回帰モデルの逐次逸脱度は、モデルによる合計逐次逸脱度を定量化します。
- 項
- 項の逐次逸脱度は、特定の項までのモデルと特定の項を含むモデルの差、項のあるモデルと項のないモデルの差を定量化します。
- 誤差
- 誤差の逐次逸脱度は、モデルでは説明できない逸脱度を定量化します。
- 合計
- 合計逐次逸脱度は、モデルの逐次逸脱度と誤差の逐次逸脱度の和です。合計逐次逸脱度はデータの合計逸脱度を定量化します。
解釈
検定のために逐次逸脱度を「使用する」に指定すると、逐次逸脱度を使用して回帰モデルのp値と各項を計算します。通常、逐次逸脱度ではなくp値を解釈します。
寄与度
寄与度には、分散分析表の各要因が合計逐次逸脱度に寄与するパーセンテージを表示します。
解釈
パーセンテージが高い場合、応答変数の中で要因が逸脱度よりも大きな割合を占めていることを示します。回帰モデルの寄与率は逸脱度R2と同じです。
調整逸脱度
調整済みの逸脱度は、モデル内の異なる構成要素の変動の測度です。モデルの予測変数の順序は調整済みの逸脱度の計算に影響を与えません。逸脱度表では、逸脱度は、異なる要因による逸脱度を説明する構成要素に分けられます。
- モデル
- 回帰モデルの調整済み逸脱度は、現在のモデルと定数モデルの差を定量化します。
- 項
- 項の調整済み逸脱度は、項のあるモデルと項のないモデルの差を定量化します。
- 誤差
- 誤差の調整済み逸脱度は、モデルでは説明できない逸脱度を定量化します。
- 合計
- 合計調整済み逸脱度は、モデルの調整済み逸脱度と誤差の調整済み逸脱度の和です。合計調整済み逸脱度はデータの合計逸脱度を定量化します。
解釈
Minitabでは、調整済み逸脱度を使用して項のp値を計算します。調整済み逸脱度を使用して、R2統計量を計算することもできます。通常、調整済み逸脱度ではなくp値とR2統計量を解釈します。
調整平均
調整済み平均逸脱度は、項またはモデルが各自由度の逸脱度をどれだけ説明づけるかを測定します。各項の調整済み平均逸脱度の計算では、モデル内にすべての他の項があると仮定します。
解釈
Minitabでは、カイ二乗値を使用して項のp値を計算します。通常は、調整平均平方の代わりにp値を解釈します。
カイ二乗
分散分析表の各項にはカイ二乗値があります。カイ二乗値は、項またはモデルに応答との関連があるかどうかを判断する検定統計量です。
解釈
Minitabではカイ二乗統計量を使用してp値を計算し、この値に基づいて、項およびモデルの統計的有意性を判断します。p値は帰無仮説を棄却するための証拠を測定する確率です。確率が低いほど、帰無仮説を棄却する強力な証拠となります。カイ二乗統計量が十分に大きいとp値は小さくなり、項またはモデルが統計的に有意であることを示します。
p値~モデル
p値は帰無仮説を棄却するための証拠を測定する確率です。確率が低いほど、帰無仮説を棄却する強力な証拠となります。
解釈
- p値 ≤ α:少なくとも1つの係数が0ではありません
- p値が有意水準以下の場合は、少なくとも1つの係数が0ではないと結論します。
- p値 > α:少なくとも1つの係数が0ではないと結論付けるだけの十分な証拠がありません
- p値が有意水準より大きい場合、少なくとも1つの係数は0ではないと結論付けることはできません。
逸脱表で表示される検定は尤度比検定です。係数表の拡張表に表示されるのはワルドの近似検定です。サンプルが小さい場合、尤度比検定のほうがワルドの近似検定よりも正確になります。
p値~項
p値は帰無仮説を棄却するための証拠を測定する確率です。確率が低いほど、帰無仮説を棄却する強力な証拠となります。
解釈
- p値 ≤ α:関連性は統計的に有意である
- p値が有意水準以下の場合は、応答変数と項の間に統計的に有意な関連性が存在すると結論付けることができます。
- p値 > α:その関連性は統計的に有意ではない
- p値が有意水準より大きい場合は、応答変数と項の間に統計的に有意な関連性があると結論することはできません。項を持たないモデルを再適合したいと考えるかもしれません。
- 連続因子が有意な場合、因子の係数は0ではないと結論できます。
- カテゴリ因子が有意である場合、事象の確率が全ての因子水準で同じではないと結論付けることができます。
- 交互作用項が有意な場合は、因子と事象確率の関係がその項の他の因子に依存すると結論付けることができます。
- 2次項が有意な場合、応答曲面が曲線を備えていると結論付けられます。
分散分析表で表示される検定は尤度比検定です。係数表の拡張表に表示されるのはワルドの近似検定です。サンプルが小さい場合、尤度比検定のほうがワルドの近似検定よりも正確になります。
p値~曲面性
p値は帰無仮説を棄却するための証拠を測定する確率です。確率が低いほど、帰無仮説を棄却する強力な証拠となります。
計画に中心点がある場合、Minitabでは曲面性の検定が行われます。モデル項と応答の関係が線形である場合、検定では平均の期待値と比較して中心点にある応答の適合平均が使用されます。曲面性をグラフ化するには、要因計画プロットを使用します。
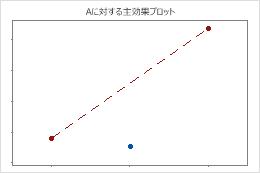
中心点は頂点の平均と交わる線から遠く離れており、曲線関係にあることを示しています。曲面性の統計的有意性をp値を用いて確認します。
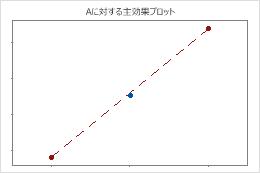
中心点は頂点の平均と交わる線の近くに配置されています。曲面性はおそらく統計的に有意ではありません。
解釈
少なくとも1つの因子が応答と曲線関係にあるかどうかを判断するには、曲面性のp値を有意水準と比較して帰無仮説を評価します。この帰無仮説は、因子と応答のすべての関係が線形であるという仮定です。
通常は、有意水準(αまたはアルファとも呼ばれる)として0.05が適切です。0.05の有意水準は、実際には実行における異なる条件は応答に影響しないにもかかわらず、影響すると結論付ける可能性が5%であることを示しています。
- p値 ≤ α: 少なくとも1つの因子が応答と曲線関係にあります
- p値が有意水準以下の場合は、少なくとも1つの因子が応答と曲線関係にあると結論付けます。曲面性をモデル化するために、計画に軸点を追加してみてください。
- p値 > α: 因子が応答と曲線関係にあると結論付けるだけの十分な証拠はありません
- p値が有意水準より大きい場合、どの因子も応答と曲線関係にあると結論付けることは出来ません。曲面性がモデルの一部である場合、曲面性が誤差の一部になるように中心点の項を抜いた状態でモデルを再適合してみてください。
注
通常、曲面性が統計的に有意でない場合は中心点の項を取り除きます。中心点をモデルに残しておくと、Minitabは要因計画で適合できない曲面性がモデルに含まれているとみなします。不適切な適合のため、等高線プロット、曲面プロット、重ね合わせ等高線プロットは利用できません。また、Minitabは応答の最適化機能による計画内に含まれる因子水準間の補完は行いません。モデルの使用方法に関する詳細は、保存モデルの概要を参照してください。
