多重比較検定
サンプルk > 2の多重比較区間
次のように定義します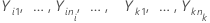 をk > 2の独立サンプルとします。各サンプルは独立していて、まったく同じように分布され、平均は
をk > 2の独立サンプルとします。各サンプルは独立していて、まったく同じように分布され、平均は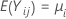 、分散は
、分散は . さらに、サンプルは共通尖度を持つ母集団から得ると仮定します。
. さらに、サンプルは共通尖度を持つ母集団から得ると仮定します。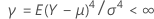
また、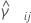 を次の式で表されるサンプルペア( i, j)の併合尖度推定とします。
を次の式で表されるサンプルペア( i, j)の併合尖度推定とします。
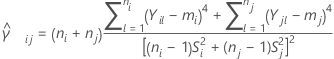
次のように定義します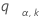 を独立で標準正規ランダム分布にまったく同じように分布される、k個の変数の幅に対する上側a点とします。つまり、
を独立で標準正規ランダム分布にまったく同じように分布される、k個の変数の幅に対する上側a点とします。つまり、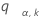 は次の式を満たします。
は次の式を満たします。
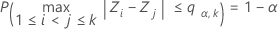
ここで、Z1, ..., Zkは互いに独立で同じ分布に従う標準正規確率変数です。バーナード(1978)の方法を使えば、16点のガウス求積法に基づくシンプルな数値アルゴリズムから、正規範囲の分布関数を求めることができます。
多重比較の手順では、次に示す区間のペアが1つも重ならない場合のみ、分散の同等性(分散の同質性とも呼ばれます)の帰無仮説が棄却されます。
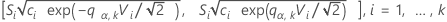
ここで、
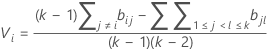
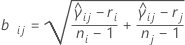
ここで、ri = (ni - 3) / niです。
上記の区間は多重比較区間またはMC区間と呼びます。各サンプルに対するMC区間は、母集団の標準偏差の信頼区間として解釈はされるものではありません。Hochbergおよびその他 (1982)は、平均を比較するための類似の区間を「不確実性区間」と呼んでいます。ここで示すMC区間はマルチサンプル計画に対する標準偏差や分散を比較するためにのみ有用です。全体の多重比較検定が有意である場合、非重複区間に対応する標準偏差は統計的に有意であると言えます。(これらの区間の派生項目の詳細については白書、多重比較の方法を参照してください。
サンプルk = 2の多重比較区間
サンプルが2つだけの場合、多重比較区間は次の式で求められます。

ここで、zα / 2は標準正規分布のα / 2番目の上側百分位数点で、ci = ni / ni - zα / 2 および Vi は次の式で求められます。
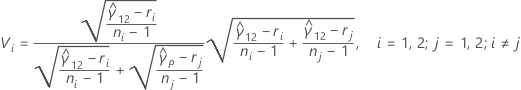
検定のp値
計画内にサンプルが2つある場合、Minitabでは2サンプルの分散検定および1の仮説の比率、Poのボネットの方法を用いて、多重比較検定用にp値が計算されます。
計画に含まれるサンプルの数がk > 2の場合、Pi jは、どのサンプルペア(i, j )にも対応する検定のp値とします。分散の同等性の全体的な検定としての多重比較手順のp値は、次の式で求められます。

シミュレーションやPi j を計算する詳細アルゴリズムを含めたさらなる情報は、ボネットの方法を参照してください。シミュレーションやボネットの方法に関する情報が記載された白書になります。
表記
| 用語 | 説明 |
|---|---|
| ni | サンプルiに含まれる観測数 |
| Y i l | サンプルiに含まれるi番目の観測値 |
| mi | サンプルiの調整平均、調整比率は、 |
| k | サンプル数 |
| Si | サンプルiの標準偏差 |
| α | テスト = 1 - (信頼水準 / 100)の有意水準 |
| Ci | 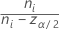 |
| Zα / 2 | 標準正規分布のα / 2番目の上側百分位数点 |
| ri |  |
ルビーンの検定統計量
Minitabでは、ルビーン検定で検定統計量とp値を表示します。帰無仮説では分散は等しく、対立仮説では分散は等しくないとします。データが連続型分布に起因し、必ずしも正規分布に起因しない場合は、ルビーン検定を使用します。
ルビーン検定の計算方法は、ブラウンおよびフォーサイス (1974)によって開発されたルビーンの方法をアレンジしたものです。この方法では、サンプル平均からではなく、サンプルの中央値からの観測値の距離が考慮されます。サンプルの中央値を使うことで、小さいサンプルに対して検定が強固になり、分析の手順は漸近的に分布が不要となります。p値がα水準よりも小さい場合、分散は等しいという帰無仮説を棄却します。
計算式
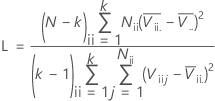
- H. Levene (1960).Contributions to Probability and Statistics.Stanford University Press, CA.
- M. B. Brown and A. B. Forsythe (1974)."Robust tests for the equality of variance," Journal of the American Statistical Association, 69, 364-367.
表記
| 用語 | 説明 |
|---|---|
| Vij |  |
| ii | 1, ..., k |
| j | 1, ..., ni |
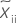 | 中央値 |
バートレットの検定統計量
Minitabでは、バートレットの検定で検定統計量とp値を表示します。水準が2つしかない場合、Minitabではバートレットの検定の代わりにF検定が実行されます。これらの検定においては、帰無仮説では分散は等しく、対立仮説では分散は等しくないとします。データが正規分布に起因するときは、バートレットの検定を使用します。バートレットの検定は、正規性から背反するほど強くはありません。
バートレットの検定統計量は、自由度に基づき各サンプル分散の重み付き算術平均および重み付き幾何平均を計算します。平均の差が大きいほど、サンプルの分散は同等ではない可能性が高くなります。Bは自由度k - 1において、χ2分布に従っています。p値がα水準よりも小さい場合、分散は等しいという帰無仮説を棄却します。
計算式
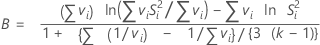
表記
| 用語 | 説明 |
|---|---|
| si2 |  |
| k | サンプル数 |
| vi | ni - 1 |
| ni | i番目の因子水準の観測値数 |
F検定統計量
水準が2つしかない場合、Minitabではバートレットの検定の代わりにF検定が実行されます。帰無仮説では分散は等しく、対立仮説では分散は等しくないとします。データが正規分布に起因するときはF統計量を使用します。
p値がα水準より小さい場合、分散は等しいという帰無仮説を棄却します。
計算式
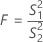
p値の計算式
- 「より小さい」対立仮説を使用した片側検定の場合、p値は自由度がDF1およびDF2のF分布の観測値以下のF統計量が得られる確率に等しくなります。
- 比が1より小さい両側検定の場合、p値は自由度がDF1およびDF2のF分布の観測値より小さいF曲線の下の部分の2倍に等しくなります。
- 比が1より大きい両側検定の場合、p値は自由度がDF1およびDF2のF分布の観測値より大きいF曲線の下の部分の2倍に等しくなります。
- 「より大きい」対立仮説を使用した片側検定の場合、p値は自由度がDF1およびDF2のF分布の観測値以上のF統計量が得られる確率に等しくなります。
表記
| 用語 | 説明 |
|---|---|
| S12 | サンプル1の分散 |
| S22 | サンプル2の分散 |
| n1 - 1 | 分子自由度 |
| n2 - 1 | 分母自由度 |
標準偏差
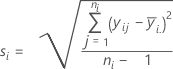
表記
| 用語 | 説明 |
|---|---|
| yij | 因子水準i番目での観測値 |
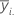 | 因子水準i番目での観測値の平均 |
| ni | i番目の因子水準の観測値数 |
ボンフェローニ信頼区間
Minitabではボンフェローニの方法を使って標準偏差の信頼区間を計算します。信頼区間は、母集団パラメータを含む可能性が高い値の範囲で、この場合では標準偏差が含まれます。
標準的な信頼区間は、信頼水準1 – α / 2で計算されますが、ボンフェローニの方法では個別信頼区間に対して信頼水準1 – α / 2pが用いられます。このときのpは因子と水準の組み合わせの数です。この方法により、信頼区間のセットの信頼水準が少なくとも1 – αであることが保証されます。ボンフェローニの方法により、第1種の過誤を犯す確率を下げる、より保守的な(広い)信頼区間が得られます。
