このトピックの内容
許容限界区間の方法
- 対数正規
- ガンマ
- 指数
- 最小極値
- ワイブル
- 最大極値
- ロジスティック
- 対数ロジスティック
一般定義
X 1、X 2、...X n は、ある連続的な分布から取られたサイズnのランダムなサンプルに基づく順序付け統計量であるとします。
次元が1以上の任意のパラメータ空間におけるΩの分布関数をF(x,θ)とします。
L < Uは、与えられる任意の値αおよびP(0 < α < 1および0 < P < 1)について、Ωにおけるすべてのθで以下が成り立つようなサンプルに基づいています。

すると、区間[L, U]はコンテンツ=P x 100%、信頼水準=100(1 – α)%の両側許容限界区間になります。このような区間は、両側(1 – α, P)の許容限界区間と呼ばれます。たとえば、α = 0.10およびP = 0.85とすると、導出される区間は、両側(90% , 0.85)の許容限界区間と呼びます。
L = –∞、およびU < +∞である場合、区間(-∞, U」は片側(1 – α, P)の上側許容限界と呼びます。L > -∞、およびU = +∞である場合、区間「L, +∞)は、片側(1 – α, P)の下側許容限界と呼びます。
- 片側(1 - α、P)の下側許容境界は、片側(P、1 - α)の上側許容限界でもあります。
- データ分布の(1 - P)番目の百分位の片側(1 - α)100%下側信頼限界は、片側(1 - α、P)の下側許容限界でもあります。同じように、データ分布のP番目の百分位の片側(1 - α)100%上側許容境界は、片側(1 - α、P)の上側許容限界でもあります。
- LとUが片側(1 – α/2 、 (1 + P )/2)の下側および上側許容限界であるならば、(L, U)は近似両側(1 – α、 P)許容限界区間になります。この方法は、両側許容限界区間を直接得られない場合に使用されることがあります。得られる両側許容限界区間は通常、保守的な結果となります。ギュンター1とハーンおよびミーカー2を参照してください。
- Guenther, W. C. (1972). Tolerance intervals for univariate distributions. Naval Research Logistics, 19: 309–333.
- Hahn G. J. and Meeker W. Q. (1991). Statistical Intervals: A Guide for Practitioners John Wiley & Sons, New York.
連続分布での正確なノンパラメトリック許容限界区間
Minitabでは、正確な(1 - α, P)ノンパラメトリック許容限界区間(1 - αは信頼水準、Pは許容限界区間のカバー範囲(区間内の母集団の目標最小パーセント))が計算されます。許容限界区間のノンパラメトリック法は分布無しの方法です。つまり、ノンパラメトリックな許容限界区間はサンプルの親母集団に依存しないということです。Minitabでは、片側区間と両側区間の両方の厳密法が使用されます。
X 1、X 2、...、X nは、ある連続的に分布する母集団F(x;θ)から取られたランダムサンプルの順序付け統計量であるとします。すると、ウィルクス1, 2とロビンズ3の結果に基づき、次のように表すことができます。

ここでBは、パラメータがa = rとb = n – s + 1のベータ分布の累積分布関数を表します。したがって、(Xr、Xs)は分布なしの許容限界区間です。これは、この区間のカバー範囲に、親母集団F(x;θ)の分布から独立した既知のパラメータ値を使用したベータ分布が含まれるからです。
片側区間
kは以下を満たす最大の整数であるとします。

ここでYは、パラメータがnおよび1 - Pの二項ランダム変数です。片側(1 – α, P)の下側許容限界は、Xk として与えられます(クリシュナマーシーおよびマシュー4を参照)。同じように、片側(1 – α, P)の上側許容限界は、X n - k +1として与えられます。どちらの場合でも、実際または有効なカバー範囲は、P(Y > k)で与えられます。
両側区間
kは、以下を満たす最小の整数であるとします。

ここでVは、パラメータがnおよびPの二項ランダム変数です。したがって、
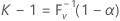
ここでF V -1(x)は、Vの逆累積分布関数です。両側(1 – α, P)の許容限界区間は、(Xr , Xs )として与えられます(クリシュナマーシーおよびマシュー4を参照)。Minitabでは、s = n - r + 1を選択し、r = (n – k + 1) / 2が成り立つようにしています。rとsは、どちらも直近の整数に切り捨てられます。実際の、すなわち有効なカバー範囲は、P(V < k – 1)で与えられます。
表記
| 用語 | 説明 |
|---|---|
| 1 – α | 許容限界区間の信頼水準 |
| P | 許容限界区間のカバー範囲(区間内の母集団の目標最小パーセント) |
| n | サンプルに含まれる観測値の数 |
- Wilks, S. S. (1941). Sample size for tolerance limits on a normal distribution. The Annals of Mathematical Statistics, 12, 91–96.
- Wilks, S. S. (1941). Statistical prediction with special reference to the problem of tolerance limits. The Annals of Mathematical Statistics, 13, 400–409.
- Robbins, H. (1944). On distribution-free tolerance limits in random sampling. The Annals of Mathematical Statistics, 15, 214–216.
- Krishnamoorthy, K. and Mathew, T. (2009). Statistical Tolerance Regions: Theory, Applications, and Computation. Wiley, Hoboken, NJ.
対数正規分布
- データの自然対数を取ります。
- 正規分布の許容限界区間の手順を用い、変換されたデータの許容限界区間を計算する。
- 前述のステップで得た許容限界区間の限界を累乗し、区間を元のデータと同じ尺度に変換する。
ガンマ分布の近似許容限界区間
ガンマ分布の許容限界区間では、正規分布の近似が使用されます。クリシュナムーシー他は近似が正確な結果を導出することを示すシミュレーションスタディーを実施しました。計算は次の工程に従います。
- データの立方根を取る。
- 正規分布の許容限界区間の手順を用い、変換されたデータの許容限界区間を計算する。
- 前述のステップで得た許容限界区間の限界を累乗し、区間を元のデータと同じ尺度に変換する。
- Krishnamoorthy K., Mathew T and Mukherjee S (2008). Normal based methods for a Gamma distribution: prediction and tolerance intervals and stress-strength reliability. Technometrics, 50, 69—78.
指数分布
Minitabでは、正確な(1 - α, P)許容限界区間が計算されます(1 - αは信頼水準、Pは許容限界区間のカバー範囲(区間内の人口の目標最小割合))。計算式は片側許容限界と両側許容限界とで異なります。
片側指数許容限界
この計算式では下限が算出されます。
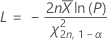
この計算式では上限が算出されます。

両側指数信頼区間
Minitabでは次の連立方程式をニュートンの方法で解きます。詳細については、フェルナンデス1を参照してください。
この計算式では両側区間が算出されます。

ここで

で、k 1の値はこの連立方程式の解に依存します。

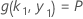
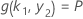
ここで、
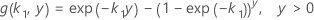
表記
| 用語 | 説明 |
|---|---|
| n | サンプルサイズ |
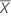 | サンプル平均 |
| P | 区間内の人口の目標最小割合 |
 | 自由度2nでのカイ二乗分布のα番目の百分位数 |
| α | 1 − 信頼水準 |
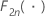 | 自由度2nでのカイ二乗分布の累積分布関数 |
- Fernandez, Arturo J. (2010). Two-sided tolerance intervals in the exponential case: Corrigenda and generalizations. Computational Statistics and Data Analysis, 54, 151~162.
最小極値分布
Minitabでは、正確な(1 - α, P)許容限界区間がローレス1に基づいて計算されます(1 - αは信頼水準、Pは許容限界区間のカバー範囲(区間内の母集団の目標最小パーセント))。
正確な片側最小極値許容限界

ここで


を次で最小化するために選択されます。

ここで

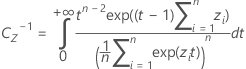

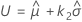
k 2の値は、k 1を算出する計算式のαを1 − α、Pを1 − Pに置き換えることで得られます。
近似両側最小極値許容限界
近似両側区間を計算するには、片側許容限界の計算式におけるαをα/2、Pを(P + 1)/2にそれぞれ置き換えます。
表記
| 用語 | 説明 |
|---|---|
 | 極値分布の位置パラメータの推定最大尤度 |
 | 極値分布の尺度パラメータの推定最大尤度 |
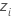 | 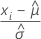 最小極値分布における位置および尺度パラメータのMLE推定に基づく中心化観測値 最小極値分布における位置および尺度パラメータのMLE推定に基づく中心化観測値 |
| t | 自由度がn − 1、非心パラメータδP の非心t分布における第α百分位数 |
| 1 - α | 許容限界区間の信頼水準 |
| P | 許容限界区間のカバー範囲(区間内の母集団の目標最小パーセント) |
| n | サンプルに含まれる観測値の数 |
- Lawless, J. F. (1975). Construction of tolerance bounds for the extreme-value and the Weibull distribution. Technometrics, 17, 255~261.
ワイブル分布
- データの自然対数を取る。
- 最小極値分布の許容限界区間の手順を用い、変換されたデータの許容限界区間を計算する。
- 前述のステップで得た許容限界区間の限界を累乗し、区間を元のデータと同じ尺度に変換する。
最大極値分布
- データに-1を掛ける。
- 最小極値分布の許容限界区間の手順を用い、変換されたデータの許容限界を計算する。
- 前述のステップで得た許容限界区間の限界を累乗し、区間を元のデータと同じ尺度に変換する。
最小極値分布に該当する計算式については、最小極値分布のセクションを参照してください。
ロジスティック分布
Minitabでは、ベインとエンゲルハルト1に基づいて近似(1 − α、 P)許容限界区間が計算されます(1 − α は信頼水準、 P はカバレッジ(区間内の母集団の目標最小パーセント)です。下限公差係数の計算式は、上限公差係数の計算式とは異なります。
片側ロジスティック許容限界
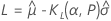

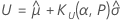

両側ロジスティック許容限界
この分析では、ボンフェローニの不等式2を使用したロジスティック分布の近似両側許容限界区間が生成されます。この近似方法は、片側公差限界を計算する式で、 α を α/2に、 P を(P + 1)/2に置き換えます。
表記
| 用語 | 説明 |
|---|---|
 | 許容係数が低い |
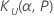 | 上限公差係数 |
| zα | 標準正規分布の上位 α 百分位数。下位1-α 百分位数に相当) |
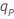 | log(p) − log(1 − p)、 p× 標準ロ ジスティック分布の100パーセンタイルが低い |
| C11 | 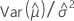 |
| C22 |  |
| C12 |  |
 | ロジスティック位置パラメータの推定最大尤度 |
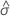 | ロジスティック尺度パラメータの推定最大尤度 |
- Bain, L. and Englehardt, M. (1991). Statistical analysis of reliability and life testing models: Theory and methods. Second edition, Marcel Dekker, Inc.
- Hahn, G. J. and Meeker, W. Q. (2017). Statistical intervals: A guide for practitioners. Second edition, John Wiley and Sons, Inc.
対数ロジスティック分布
- データの自然対数を取る。
- ロジスティック分布の許容限界区間の手順を用い、変換されたデータの許容限界区間を計算する。
- 前述のステップで得た許容限界区間の限界を累乗し、区間を元のデータと同じ尺度に変換する。
ロジスティック分布に該当する計算式については、ロジスティック分布のセクションを参照してください。
アンダーソン-ダーリング検定
Minitabでは、アンダーソン-ダーリング統計量を使用して適合度検定を実行します。
Z = F(X)で、F(X)は累積分布関数であるとします。サンプルのX1, .., Xnは、Z(i) = F(Xi), i=1,.., nを示すと仮定します。Z(i)をZ(1) < Z(2) <...<Z(n)の昇順で並び替えます。すると、アンダーソン-ダーリング検定の(A2)は次のように計算されます。
- A2 = –n - (1/n) Σi[(2i – 1) log Z(i) + (2n + 1 – 2i) log (1 – Z(i))]
修正されたアンダーソンーダーリングの適合度検定の統計量が各分布に対して計算されます。p値はダゴスティーノおよびステファンズの表に基づきます。1表に正確なp値がない場合、Minitabではp値の範囲を用いた内挿法に基づいてp値が計算されます。
