非正規データに対して使用可能な分析
- データに適合する非正規分布モデルを選択し、 などの 非正規能力分析非正規データの工程能力分析を使用してデータを分析します。
- 正規分布が適切なモデルになるようにデータを変換し、正規 正規工程能力分析データに対して工程能力分析を使用します。
- データの分布を前提としないノンパラメトリックな方法を選択します工程能力分析(ノンパラメトリック)。
- 工程の工学的および経験的知識を活用します。
- ほとんどの場合、工程データに適合するメソッドを特定するには、工学的および経験的な知識を活用することが推奨されます。たとえば、データは対称分布に従っていますか。同様の状況で過去にどのような方法が機能しましたか?
- 適合度評価を使用します。
- アンダーソン-ダーリング検定は、特定の分布が工程のデータに適合するかどうかを評価します。確率プロットは、データが分布にどの程度厳密に従っているかを評価する別のツールです。
- さまざまな方法が結論にどのように影響するかを評価します。
- いくつかの方法がデータと同様の結論に適切に適合する場合、選択はそれほど重要ではありません。逆に、結論が方法に依存する場合は、最も保守的な結論を報告するか、より多くの情報を収集することをお勧めします。たとえば、分布 自動工程能力分析 の結果または百 個別の分布の識別 分位数を使用して、結論が方法にどのように依存するかを確認できます。
- 経時的に工程能力分析を繰り返し実行する場合は、長期にわたって一貫して工程を適切に特徴付ける方法を使用するようにしてください。同じ方法を使用すると、繰り返し分析のインデックスを簡単かつ直接比較できます。
- 非正規モデルとノンパラメトリック モデルでは、実際のデータ単位が使用されます。変換の法線モデルでは、変換された単位が使用されます。
- 変換の正規モデルは、全体工程能力と工程能力内工程能力の両方の推定値を提供します。
自動工程能力分析 Minitab統計ソフトウェアを使用して、方法の有用性と実用性を考慮しながら、データに適合する合理的な方法を決定するのに役立ちます。分析では、最初に分布が考慮され、次に変換が考慮されます。データに適合するモデルがない場合、分析ではノンパラメトリックな方法が使用されます。
データの詳細を確認するには、を使用します 個別の分布の識別。この分析では、さまざまな方法の適合度の測度が提供され、使用する方法の決定がサポートされます。
メソッドを選択するために使用します 自動工程能力分析
複数の方法とデータの互換性を評価し、妥当な選択を行うために使用します 自動工程能力分析 。
- を選択します 。
- データを 1 つの列に配置するか、複数の行に配置するかを指定します。
- 工程の規格限界を入力します。
分析では、分布が考慮され、次に変換が考慮されます。データに適合するパラメトリックな方法がない場合、分析ではノンパラメトリックな方法が使用されます。結果には、妥当な適合を提供する最初の方法の工程能力レポートが含まれます。分布結果の表には、方法の評価順序、方法の適合度に関する情報、および工程能力統計量が表示されます。別の方法の結果を生成して、メソッドをより詳細に調査できます。
自動工程能力分析 メソッドの選択に使用する例
エンジニアは、セラミックタイルの反りの程度に関するデータを収集します。データの分布は不明であるため、データに対して実行 個別の分布の識別 して、工程能力分析の妥当な方法を決定します。
分布結果の表は、方法の評価の順序を示しています。最初の行では、アンダーソン-ダーリング検定の結論は、p値が0.05未満であるため、データは有意水準0.05の正規分布に従わないというものです。2行目のアンダーソン-ダーリング検定の結論は、p値が0.05より大きいため、ワイブル分布がデータに合理的に適合するということです。ワイブル分布が妥当な適合を提供するリストの最初の方法であるため、工程能力の結果はワイブル分布に対するものです。
エンジニアは、工程の知識を使用して、ワイブル分布が妥当な方法であるかどうかを検討します。たとえば、ワイブル分布の境界は 0 です。データでは、0 はワープされていないタイルを表す境界です。
分析には、ワイブル分布を使用する工程能力分析が含まれます。
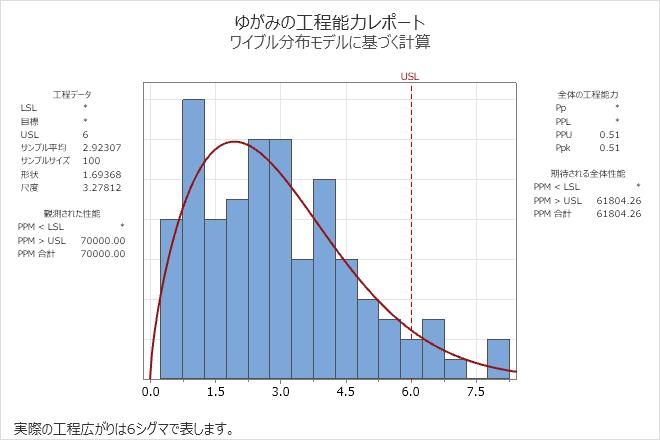
自動工程能力分布の結果: ゆがみ
| 分布 | 位置 | 尺度 | 閾値 | 形状 | p値 | Ppk | Cpk |
|---|---|---|---|---|---|---|---|
| 正規 | 2.9231 | 1.7860 | 0.0100421 | 0.5743 | 0.5838 | ||
| ワイブル* | 3.2781 | 1.6937 | >0.25 | 0.5133 | |||
| 対数正規 | 0.8443 | 0.7444 | <0.005 | 0.4242 | |||
| 最小極値 | 3.8641 | 1.9924 | <0.01 | 0.5362 | |||
| 最大極値 | 2.0958 | 1.4196 | 0.212835 | 0.5130 | |||
| ガンマ | 1.2477 | 2.3428 | 0.238337 | 0.4851 | |||
| ロジスティック | 2.7959 | 1.0162 | 0.0127347 | 0.5799 | |||
| 対数ロジスティック | 0.9097 | 0.4217 | <0.005 | 0.4090 | |||
| 指数 | 2.9231 | <0.0025 | 0.3780 | ||||
| 3-パラメータワイブル | 2.9969 | 0.2099 | 1.5049 | 0.467097 | 0.4980 | ||
| 3-パラメータ対数正規 | 1.3788 | 0.4184 | -1.4002 | 0.4961 | |||
| 3-パラメータガンマ | 1.2314 | -0.0197 | 2.3898 | 0.4864 | |||
| 3-パラメータ対数ロジスティック | 1.3043 | 0.2700 | -1.0940 | 0.4656 | |||
| 2-パラメータ指数 | 2.6679 | 0.2552 | <0.01 | 0.3982 | |||
| Box-Cox変換 | 1.6237 | 0.5380 | 0.574337 | 0.5116 | 0.5214 | ||
| Johnson変換 | 0.0112 | 0.9949 | 0.798895 | 0.4959 | |||
| ノンパラメトリック | 0.6187 |
適切な分布または変換を見つけるために使用します 個別の分布の識別
工程能力分析を実行する前に、 個別の分布の識別 データに最も適した分布または変換を決定します。データと互換性のある分布または変換がない場合は、 を検討してください 工程能力分析(ノンパラメトリック)。
- を選択します。
- データが1列に配置されているのが、または複数の行にまたがっているのかを選択します。
- [OR 指定する ] を選択し すべての分布と変換を使用 、テストする分布と変換を最大 4 つ選択します。
- 非正規能力分析
- 多重変数の非正規工程能力分析
- 非正規工程能力シックスパック
- 正規工程能力分析
- 正規工程能力シックスパック
- 多重変数の正規工程能力分析
- 工程能力分析間/内
個別の分布の識別 分布と変換の適合度を比較するために使用する例
エンジニアは、セラミックタイルの反りの程度に関するデータを収集します。データ分布は不明であるため、データに対して実行 個別の分布の識別 して、ジョンソン変換後の指数分布と正規分布の適合度を比較します。
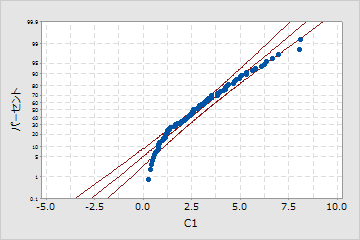
指数分布
この確率プロットは、指数分布が適合しないことを示しています。
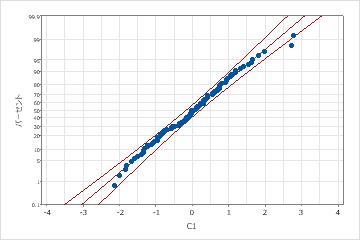
Johnson変換を適用した正規分布
しかし、Johnson変換を適用すると、p値が大きく、ほぼすべてのデータ点が正規確率プロットの信頼限界内に含まれるので、データは正規分布にかなり近くなります。
