区間プロットの主要な結果を解釈する

区間の上にポインタを置くと、推定平均や信頼区間、サンプルサイズを表示するためのツールチップが表示されます。たとえば、この区間プロットは生徒の身長を表します。ツールチップは、身長の平均が67.9591～69.4914だと95%信頼できることを示しています。

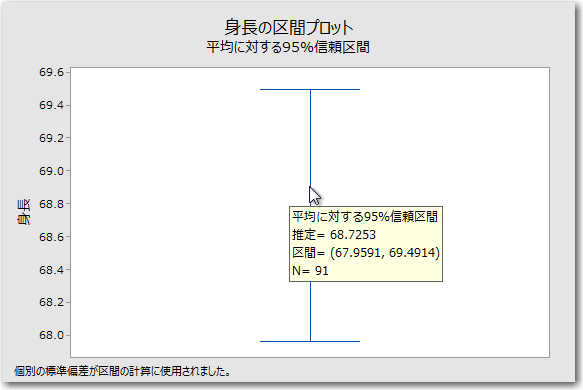
異常な、あるいは予期せぬ信頼区間を調査します。たとえば、顧客の待ち時間のサンプル平均の信頼区間が前回のサンプルの信頼区間とはかなり異なる場合、差の原因を特定する必要があります。

サンプルサイズはグラフの表示に作用する可能性があります。

たとえば、これらの区間はかなり異なっているように見えますが、どちらも同じ母集団から無作為に選ばれたデータのサンプルを使用して作成されています。

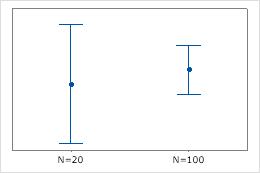
通常、サンプルサイズが大きくなるほど、信頼区間は小さく精度も高くなります。信頼区間が広すぎる場合、より大きなサンプルを収集してみてください。グループ（または複数のY変数）間のサンプルサイズの差が大きい場合、区間の幅に影響を与えることがあり、誤解を生みやすい結果になる可能性があります。グループ（または複数のY変数）のサンプルサイズがほぼ同じ場合、区間の幅の差が主に分散の差に起因するということは、より信頼できるようになります。

信頼区間に重なりがあるかどうかを判定します。2つの平均の区間に重なりがない場合、母平均は統計的に有意である可能性があります。

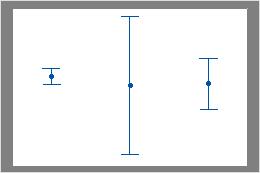
たとえば、最初の区間プロットの1番目と2番目の区間には重なりがありますが3番目の区間とは重なりがありません。したがって、3番目のグループの平均は、他の2つのグループの平均とは大きく異なることがあります。2番目の区間プロットでは区間に重なりはありません。したがって、平均の差は統計的に有意である可能性があります。

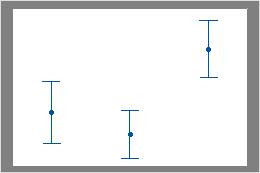
重なり合う区間あり

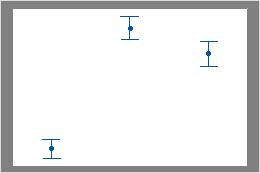
重なり合う区間なし

グループの広がりの間の差を探します。

このプロットの区間では中心は似通っていますが分布は異なります。