Example for Cluster Observations

A designer for a sporting goods company wants to test a new soccer goalie glove. The designer has 20 athletes wear the new glove and collects the gender, height, weight, and handedness information of the athletes. The designer wants to group the athletes by their similarities.

Open the sample data set, GloveTesters.MWX.
Choose Stat > Multivariate > Cluster Observations.
In Variables or distance matrix, enter Gender Height Weight Handedness.
From Linkage method, select Complete. From Distance measure, select Euclidean.
Select Standardize variables.
Select Show dendrogram.
Click OK.

Interpret the results

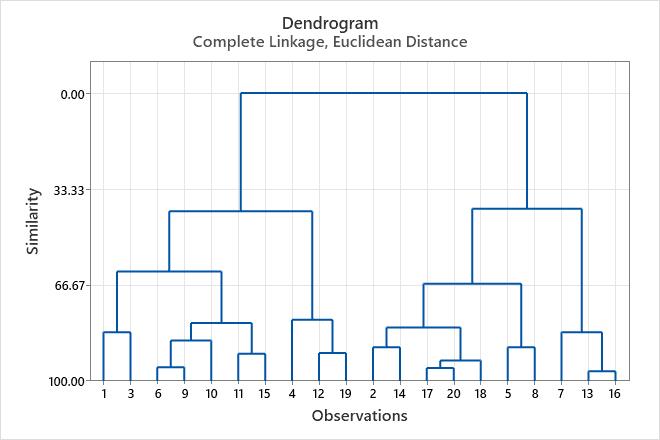
The table shows the clusters that were joined at each step, the distance between the clusters, and the similarity of the clusters.

The similarity level decreases by increments of approximately 3 or less until step 15. The similarity decreases by more than 20 (from 62.0036 to 41.0474) at steps 16 and 17, when the number of clusters changes from 4 to 3.
The distance between the joined clusters increases, first by approximately 0.6 or less. The distance increases by more than 1 (from 1.81904 to 2.82229) at steps 16 and 17, when the number of clusters changes from 4 to 3.

The distance and similarity results indicate that 4 clusters are reasonably sufficient for the final partition. If this grouping makes intuitive sense to the designer, then it is probably a good choice. The dendrogram displays the information in the table in the form of a tree diagram.

The designer should rerun the analysis and specify 4 clusters in the final partition. When you specify a final partition, Minitab displays additional tables that describe the characteristics of each cluster that is included in the final partition.

Step	Number of clusters	Similarity level	Distance level	Clusters joined		New cluster	Number of obs. in new cluster
1	19	96.6005	0.16275	13	16	13	2
2	18	95.4642	0.21715	17	20	17	2
3	17	95.2648	0.22669	6	9	6	2
4	16	92.9178	0.33905	17	18	17	3
5	15	90.5296	0.45339	11	15	11	2
6	14	90.3124	0.46378	12	19	12	2
7	13	88.2431	0.56285	2	14	2	2
8	12	88.2431	0.56285	5	8	5	2
9	11	85.9744	0.67146	6	10	6	3
10	10	83.0639	0.81080	7	13	7	3
11	9	83.0639	0.81080	1	3	1	2
12	8	81.4039	0.89027	2	17	2	5
13	7	79.8185	0.96617	6	11	6	5
14	6	78.7534	1.01716	4	12	4	3
15	5	66.2112	1.61760	2	5	2	7
16	4	62.0036	1.81904	1	6	1	7
17	3	41.0474	2.82229	1	4	1	10
18	2	40.1718	2.86421	2	7	2	10
19	1	0.0000	4.78739	1	2	1	20

Example for Cluster Observations

Interpret the results

Amalgamation Steps

Final Partition