In This Topic
Deviance R2
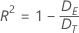
Notation
| Term | Description |
|---|---|
| DE | Error Deviance |
| DT | Total Deviance |
Adjusted Deviance R2

Notation
| Term | Description |
|---|---|
| R2 | the deviance R2 |
| p | the regression degrees of freedom |
| Φ | 1, for binomial and Poisson models |
| DT | the total deviance |
While the calculations for adjusted deviance R2 can produce negative values, Minitab displays zero for these cases.
Akaike Information Criterion (AIC)
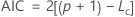
The log-likelihood functions are parameterized in terms of the means. The general form of the functions follow:
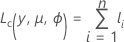
The general form of the individual contributions follows:

The specific form of the individual contributions depends on the model.
| Model | li |
| Binomial | 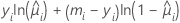 |
| Poisson |  |
Notation
| Term | Description |
|---|---|
| p | the regression degrees of freedom |
| Lc | the log-likelihood of the current model |
| yi | the number of events for the ith row |
| mi | the number of trials for the ith row |
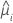 | the estimated mean response of the ith row |
AICc (Akaike's Corrected Information Criterion)

AICc is not calculated when  .
.
Notation
| Term | Description |
|---|---|
| p | the number of coefficients in the model, including the constant |
| n | the number of rows in the data with no missing data |
BIC (Bayesian Information Criterion)

Notation
| Term | Description |
|---|---|
| p | the number of coefficients in the model, not counting the constant |
| n | the number of rows in the data with no missing data |
Test deviance R2
Formula
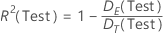
where the following equation represents the error deviance:
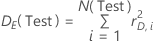
- Binary logistic
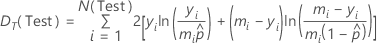
- Poisson

Notation
| Term | Description |
|---|---|
| N(Test) | the number of rows in the test data set |
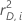 | the squared deviance residuals |
| yi | the number of events for the ith row in the test data set |
| mi | the number of trials for the ith row in the test data set |
| DE(Test) | the error deviance for the test data set |
| DT(Test) | the total deviance for the test data set |
K-fold Deviance R2

Where
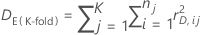
and DT is the total deviance.
Notation
| Term | Description |
|---|---|
| K | number of folds |
| nj | sample size of fold j |
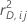 | cross validated deviance residual for the ith row of fold j |
Area under ROC curve
Formula


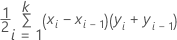
where k is the number of distinct event probabilities and (x0, y0) is the point (0, 0).
To compute the area for a curve from a test data set or from cross-validated data, use the points from the corresponding curve.
| x (false positive rate) | y (true positive rate) |
|---|---|
| 0.0923 | 0.3051 |
| 0.4154 | 0.7288 |
| 0.7538 | 0.9322 |
| 1 | 1 |
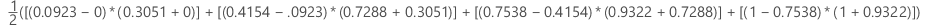

Notation
| Term | Description |
|---|---|
| TRP | true positive rate |
| FPR | false positive rate |
| TP | true positive, events that were correctly assessed |
| P | number of actual positive events |
| FP | true negative, nonevents that were correctly assessed |
| N | number of actual negative events |
| FNR | false negative rate |
| TNR | true negative rate |