In This Topic
Mean
A commonly used measure of the center of a batch of numbers. The mean is also called the average. It is the sum of all observations divided by the number of (nonmissing) observations.
Formula
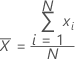
Notation
| Term | Description |
|---|---|
| xi | ith observation |
| N | number of nonmissing observations |
Standard deviation (StDev)
The sample standard deviation provides a measure of the spread of your data. It is equal to the square root of the sample variance.
Formula
 , then the standard deviation of the sample is:
, then the standard deviation of the sample is:
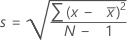
Notation
| Term | Description |
|---|---|
| x i | i th observation |
 | mean of the observations |
| N | number of nonmissing observations |
Variance
The variance measures how spread out the data are about their mean. The variance is equal to the standard deviation squared.
Formula
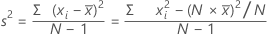
Notation
| Term | Description |
|---|---|
| xi | ith observation |
 | mean of the observations |
| N | number of nonmissing observations |
Sum
Formula

Notation
| Term | Description |
|---|---|
| xi | i th observation |
Minimum
The smallest value in your data set.
Median
The sample median is in the middle of the data: at least half the observations are less than or equal to it, and at least half are greater than or equal to it.
Suppose you have a column that contains N values. To calculate the median, first order your data values from smallest to largest. If N is odd, the sample median is the value in the middle. If N is even, the sample median is the average of the two middle values.
For example, when N = 5 and you have data x1, x2, x3, x4, and x5, the median = x3.
When N = 6 and you have ordered data x1, x2, x3, x4, x5,and x6:

where x3 and x4 are the third and fourth observations.
Maximum
The largest value in your data set.
Average
Formula
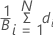
Notation
| Term | Description |
|---|---|
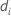 | difference in means of the ith resamples |
| B | number of resamples |
| N | number of observations for one group in the original sample |
Standard deviation of the bootstrapping distribution
Formula

Notation
| Term | Description |
|---|---|
 | mean of the differences of the resamples |
| B | number of resamples |
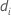 | difference in means of the ith resample |
P-Value
Formula
- Mean less than hypothesized value:
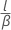
- Mean not equal to hypothesized value:
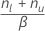
- Mean greater than hypothesized value:

Notation
| Term | Description |
|---|---|
| l | number of bootstrap differences in means that are less than or equal to d |
| u | number of bootstrap differences in means that are greater than or equal to d |
| β | number of resamples |
| nl | number of bootstrap differences in means that are less than or equal to −d |
| nu | number of bootstrap differences in means that are greater than or equal to d |
| d | sample difference in means |
