Fabric appraisers at a textile printing company rate the print quality of cotton fabric on a 1 to 5 point scale. The quality engineer wants to assess the consistency and correctness of the appraisers' ratings. The engineer asks four appraisers to rate print quality on 50 samples of fabric twice, in random order.
Because the data include a known standard for each sample, the quality engineer can assess the consistency and correctness of ratings compared to the standard as well as compared to other appraisers.
- Open the sample data, TextilePrintQuality.MTW.
- Choose .
- In Data are arranged as, select Attribute column and enter Response.
- In Samples, enter Sample.
- In Appraisers, enter Appraiser.
- In Known standard/attribute, enter Standard.
- Select Categories of the attribute data are ordered.
- Click OK.
Interpret the results
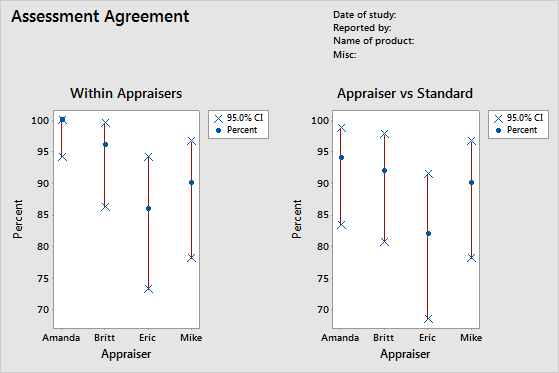
- Within Appraisers table
- Because each appraiser provides two or more ratings for each sample, the engineer can evaluate the consistency of each appraiser.
- Each Appraiser vs Standard table
- Because there is a known standard for each sample, the engineer can evaluate the accuracy and consistency of each of the appraiser's ratings.
- Between Appraisers table
- The Between Appraisers table shows that the appraisers agree on their ratings for 37 of the 50 samples.
- All Appraisers vs Standard table
- Because there is a known standard for each sample, the engineer can evaluate the accuracy of all the appraisers' ratings.
Note
The p-value of 0.0000 in the output is rounded. But you can safely conclude that the p-value is very low and is < 0.00005.
Attribute Agreement Analysis for Response
Within Appraisers
Assessment Agreement
Appraiser # Inspected # Matched Percent 95% CI
Amanda 50 50 100.00 (94.18, 100.00)
Britt 50 48 96.00 (86.29, 99.51)
Eric 50 43 86.00 (73.26, 94.18)
Mike 50 45 90.00 (78.19, 96.67)
# Matched: Appraiser agrees with him/herself across trials.
Fleiss’ Kappa Statistics
Appraiser Response Kappa SE Kappa Z P(vs > 0)
Amanda 1 1.00000 0.141421 7.0711 0.0000
2 1.00000 0.141421 7.0711 0.0000
3 1.00000 0.141421 7.0711 0.0000
4 1.00000 0.141421 7.0711 0.0000
5 1.00000 0.141421 7.0711 0.0000
Overall 1.00000 0.071052 14.0741 0.0000
Britt 1 1.00000 0.141421 7.0711 0.0000
2 0.89605 0.141421 6.3360 0.0000
3 0.86450 0.141421 6.1129 0.0000
4 1.00000 0.141421 7.0711 0.0000
5 1.00000 0.141421 7.0711 0.0000
Overall 0.94965 0.071401 13.3002 0.0000
Eric 1 0.83060 0.141421 5.8733 0.0000
2 0.84000 0.141421 5.9397 0.0000
3 0.70238 0.141421 4.9666 0.0000
4 0.70238 0.141421 4.9666 0.0000
5 1.00000 0.141421 7.0711 0.0000
Overall 0.82354 0.071591 11.5034 0.0000
Mike 1 1.00000 0.141421 7.0711 0.0000
2 0.83060 0.141421 5.8733 0.0000
3 0.81917 0.141421 5.7924 0.0000
4 0.86450 0.141421 6.1129 0.0000
5 0.86450 0.141421 6.1129 0.0000
Overall 0.87472 0.070945 12.3295 0.0000
Kendall’s Coefficient of Concordance
Appraiser Coef Chi - Sq DF P
Amanda 1.00000 98.0000 49 0.0000
Britt 0.99448 97.4587 49 0.0000
Eric 0.98446 96.4769 49 0.0001
Mike 0.98700 96.7256 49 0.0001
Each Appraiser vs Standard
Assessment Agreement
Appraiser # Inspected # Matched Percent 95% CI
Amanda 50 47 94.00 (83.45, 98.75)
Britt 50 46 92.00 (80.77, 97.78)
Eric 50 41 82.00 (68.56, 91.42)
Mike 50 45 90.00 (78.19, 96.67)
# Matched: Appraiser’s assessment across trials agrees with the known standard.
Fleiss’ Kappa Statistics
Appraiser Response Kappa SE Kappa Z P(vs > 0)
Amanda 1 1.00000 0.100000 10.0000 0.0000
2 0.83060 0.100000 8.3060 0.0000
3 0.81917 0.100000 8.1917 0.0000
4 1.00000 0.100000 10.0000 0.0000
5 1.00000 0.100000 10.0000 0.0000
Overall 0.92476 0.050257 18.4006 0.0000
Britt 1 1.00000 0.100000 10.0000 0.0000
2 0.83838 0.100000 8.3838 0.0000
3 0.80725 0.100000 8.0725 0.0000
4 1.00000 0.100000 10.0000 0.0000
5 1.00000 0.100000 10.0000 0.0000
Overall 0.92462 0.050396 18.3473 0.0000
Eric 1 0.91159 0.100000 9.1159 0.0000
2 0.81035 0.100000 8.1035 0.0000
3 0.72619 0.100000 7.2619 0.0000
4 0.84919 0.100000 8.4919 0.0000
5 1.00000 0.100000 10.0000 0.0000
Overall 0.86163 0.050500 17.0622 0.0000
Mike 1 1.00000 0.100000 10.0000 0.0000
2 0.91694 0.100000 9.1694 0.0000
3 0.90736 0.100000 9.0736 0.0000
4 0.92913 0.100000 9.2913 0.0000
5 0.93502 0.100000 9.3502 0.0000
Overall 0.93732 0.050211 18.6674 0.0000
Kendall’s Correlation Coefficient
Appraiser Coef SE Coef Z P
Amanda 0.967386 0.0690066 14.0128 0.0000
Britt 0.967835 0.0690066 14.0193 0.0000
Eric 0.951863 0.0690066 13.7879 0.0000
Mike 0.975168 0.0690066 14.1256 0.0000
Between Appraisers
Assessment Agreement
# Inspected # Matched Percent 95% CI
50 37 74.00 (59.66, 85.37)
# Matched: All appraisers’ assessments agree with each other.
Fleiss’ Kappa Statistics
Response Kappa SE Kappa Z P(vs > 0)
1 0.954392 0.0267261 35.7101 0.0000
2 0.827694 0.0267261 30.9695 0.0000
3 0.772541 0.0267261 28.9058 0.0000
4 0.891127 0.0267261 33.3429 0.0000
5 0.968148 0.0267261 36.2248 0.0000
Overall 0.881705 0.0134362 65.6218 0.0000
Kendall’s Coefficient of Concordance
Coef Chi - Sq DF P
0.976681 382.859 49 0.0000
All Appraisers vs Standard
Assessment Agreement
# Inspected # Matched Percent 95% CI
50 37 74.00 (59.66, 85.37)
# Matched: All appraisers’ assessments agree with the known standard.
Fleiss’ Kappa Statistics
Response Kappa SE Kappa Z P(vs > 0)
1 0.977897 0.0500000 19.5579 0.0000
2 0.849068 0.0500000 16.9814 0.0000
3 0.814992 0.0500000 16.2998 0.0000
4 0.944580 0.0500000 18.8916 0.0000
5 0.983756 0.0500000 19.6751 0.0000
Overall 0.912082 0.0251705 36.2362 0.0000
Kendall’s Correlation Coefficient
Coef SE Coef Z P
0.965563 0.0345033 27.9817 0.0000