To use these functions, choose .
The Gamma, Incomplete gamma, and Natural log of gamma functions extend the factorial function (1 * 2 * 3...* n) so that factorials can be calculated for fractions in addition to positive integers. The Natural log of gamma function is sometimes used in calculations instead of the gamma function because the Natural log of gamma is less likely to generate very large numbers that can be larger than the storage capability and cause overflow.
Syntax
- GAMMA(shape)
- IGAMMA(limit,shape)
- LNGAMMA(shape)
For shape, specify the number you want to take the function of. For limit, specify the upper limit of the integral.
Examples
| Calculator expression | Result |
|---|---|
| GAMMA(0.5) | 1.77245 |
| IGAMMA(1,2) | 0.264241 |
| LNGAMMA(3.5) | 1.20097 |
Formulas
 , is also called the generalized factorial function and is defined as:
, is also called the generalized factorial function and is defined as:
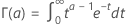
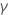 , is a variation of the complete gamma function defined by an integral with a finite, instead of an infinite, upper bound. For a given number a and an upper bound x,
, is a variation of the complete gamma function defined by an integral with a finite, instead of an infinite, upper bound. For a given number a and an upper bound x,
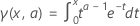
The Natural log of gamma function,  , is the natural log of the complete gamma function.
, is the natural log of the complete gamma function.
Note
The Complete gamma function is undefined when the variable a equals a negative integer or zero. The Incomplete gamma function is undefined when the variable a equals any negative number or zero. Minitab returns a missing value * when the Gamma function of a number is undefined.
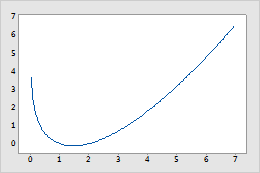
Lngamma function
Natural log gamma is a convex function defined only for positive numbers.
Uses
The Gamma function is important in pure and applied mathematics, science, and engineering, including applications involving heat conduction in lasers and human tissues. In statistics, the gamma function is used to calculate the probability density function and cumulative distribution function of the gamma distribution, which can be used to describe positively skewed data.
