Remarque
Cette commande est disponible avec la commande Module d'analyse prédictive. Cliquez ici pour plus d’informations sur la façon d’activer le module.
Recherche du meilleur type de modèle
Une équipe de chercheurs recueille et publie des informations détaillées sur les facteurs qui affectent les maladies cardiaques. Les variables comprennent l’âge, le sexe, le taux de cholestérol, la fréquence cardiaque maximale, etc. Cet exemple est basé sur un ensemble de données publiques qui fournit des informations détaillées sur les maladies cardiaques. Les données originales proviennent de archive.ics.uci.edu.
Les chercheurs veulent trouver un modèle qui fait les prédictions les plus précises possibles. Les chercheurs utilisent Découvrir le meilleur modèle (réponse binaire) pour comparer les performances prédictives de 4 types de modèles : la régression logistique binaire, TreeNet®, Random Forests® et CART®. Les chercheurs prévoient d’explorer davantage le type de modèle offrant les meilleures performances prédictives.
- Ouvrez les données d’échantillonnage, MaladieCardiaqueBinaireMeilleurModele.MWX.
- Choisissez .
- Dans Réponse, entrez 'Maladies cardiaques'.
- Dans Prédicteurs continus, entrez Âge, 'Pression artérielle de repos', Cholestérol', 'Fréquence cardiaque maximale' et ' Vieux pic'.
- Dans Prédicteurs de catégorie, entrez Sexe, ' Type de douleur thoracique', 'Sucre de sang de jeûne', 'Repos ECG', 'Exercice Angina', Pente, 'Principaux navires', et Thal.
- Cliquez sur OK.
Interpréter les résultats
Le tableau de sélection de modèles compare les performances des différents types de modèles. Le modèle Random Forests® a la valeur minimale de la loglogicabilité moyenne. Les résultats qui suivent sont pour le meilleur modèle Random Forests®.
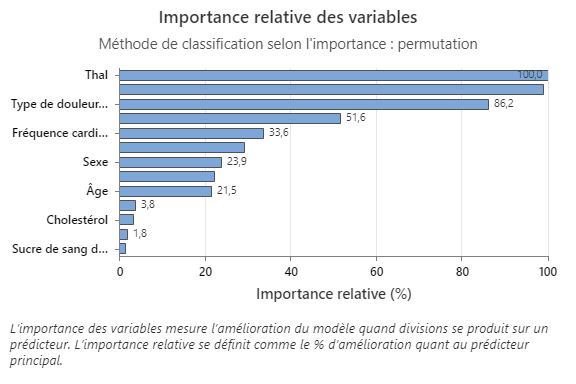
Le graphique Taux d’erreur de classification en fonction du nombre d’arbres montre la courbe entière sur le nombre d’arbres cultivés. Le taux d’erreurs de classification est d’environ 0,16.
Le tableau récapitulatif du modèle montre que le log-vraisemblance négatif moyen est d’environ 0,39.
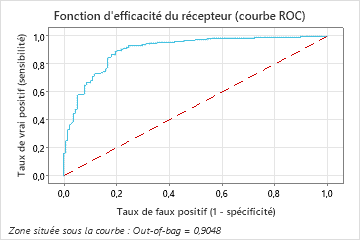
Le graphique Importance relative des variables trace les prédicteurs dans l’ordre de leur effet sur l’amélioration du modèle lorsque des divisions sont effectuées sur un prédicteur au cours de la séquence d’arbres. La variable prédictive la plus importante est Thal. Si la contribution de la variable prédictive principale, Thal, est de 100 %, la variable importante suivante, Major Vessels, a une contribution de 98,9 %. Cela signifie que les grands navires sont 98,9 % aussi importants que Thal dans ce modèle de classification.
La matrice de confusion montre dans quelle mesure le modèle sépare correctement les classes. Dans cet exemple, la probabilité qu’un événement soit prédit correctement est d’environ 87 %. La probabilité qu’un non-événement soit prédit correctement est d’environ 81 %.
Le taux d’erreurs de classification permet d’indiquer si le modèle prédira avec précision les nouvelles observations. Pour la prédiction des événements, l’erreur de classification hors sac est d’environ 13 %. Pour la prédiction des non-événements, l’erreur de classification erronée est d’environ 19 %. Dans l’ensemble, l’erreur de classification des données de test est d’environ 16 %.
L’aire sous la courbe ROC pour le modèle Random Forests® est d’environ 0,90 pour les données prêtes à l’emploi.
Méthode
| Ajustez un modèle de régression logistique pas à pas avec des termes linéaires et des termes d'ordre 2. |
|---|
| Ajustez 6 modèles de classification TreeNet®. |
| Ajustez 3 modèle(s) de classification Random Forests® avec un effectif d'échantillon bootstrap identique à la taille des données d'apprentissage de 303. |
| Ajuster un modèle de classification CART® optimal. |
| Sélectionnez le modèle avec une valeur de log de vraisemblance maximale d'après la validation croisée sur 5 partitions. |
| Nombre total de lignes : 303 |
| Lignes utilisées pour le modèle de régression logistique : 303 |
| Lignes utilisées pour les modèles basés sur des arbres : 303 |
Informations de réponse binaire
| Variable | Classe | Dénombrement | % |
|---|---|---|---|
| Maladies cardiaques | 1 (Événement) | 165 | 54,46 |
| 0 | 138 | 45,54 | |
| Tous | 303 | 100,00 |
| Meilleur modèle pour le type | Log de vraisemblance de moyenne | Zone située sous la courbe ROC | Taux de classification erronée |
|---|---|---|---|
| Random Forests®* | 0,3904 | 0,9048 | 0,1584 |
| TreeNet® | 0,3907 | 0,9032 | 0,1520 |
| Régression logistique | 0,4671 | 0,9142 | 0,1518 |
| CART® | 1,8072 | 0,7991 | 0,2080 |
Hyperparamètres pour le meilleur modèle Random Forests®
| Nombre d'échantillons bootstrap | 300 |
|---|---|
| Effectif d'échantillon | Identique à la taille des données d'apprentissage de 303 |
| Nombre de prédicteurs sélectionnés pour la partition des nœuds | Racine carrée du nombre total de prédicteurs = 3 |
| Taille minimale du nœud interne | 8 |
Récapitulatif du modèle
| Nombre total de prédicteurs | 13 |
|---|---|
| Prédicteurs importants | 13 |
| Statistiques | Out-of-Bag |
|---|---|
| Log de vraisemblance de moyenne | 0,3904 |
| Zone située sous la courbe ROC | 0,9048 |
| IC à 95 % | (0,8706; 0,9389) |
| Lift | 1,7758 |
| Taux de mauvaise classification | 0,1584 |
Matrice de confusion
| Catégorie prévue (Out-of-Bag) | ||||
|---|---|---|---|---|
| Classe réelle | Dénombrement | 1 | 0 | % correct |
| 1 (Événement) | 165 | 143 | 22 | 86,67 |
| 0 | 138 | 26 | 112 | 81,16 |
| Tous | 303 | 169 | 134 | 84,16 |
| Statistiques | Out-of-Bag (%) |
|---|---|
| Taux de vrai positif (sensibilité ou puissance) | 86,67 |
| Taux de faux positif (erreur de type I) | 18,84 |
| Taux de faux négatif (erreur de type II) | 13,33 |
| Taux de vrai négatif (spécificité) | 81,16 |
Mauvais classement
| Out-of-Bag | |||
|---|---|---|---|
| Classe réelle | Dénombrement | Mal classé | % erreur |
| 1 (Événement) | 165 | 22 | 13,33 |
| 0 | 138 | 26 | 18,84 |
| Tous | 303 | 48 | 15,84 |
Sélectionnez un modèle alternatif
Les chercheurs peuvent examiner les résultats d’autres modèles à partir de la recherche du meilleur modèle. Pour un modèle TreeNet®, vous pouvez sélectionner un modèle qui faisait partie de la recherche ou spécifier des hyperparamètres pour un autre modèle.
- Sélectionnez Sélectionner un autre modèle.
- Dans Type de modèle, sélectionnez TreeNet®.
- Dans Sélectionner un modèle existant, choisissez le troisième modèle, qui a la meilleure valeur de la moyenne minimale –loglogsemblabilité.
- Cliquez sur Afficher les résultats.
Interpréter les résultats
Cette analyse fait pousser 300 arbres et le nombre optimal d’arbres est de 46. Le modèle utilise un taux d’apprentissage de 0,1 et une fraction de sous-échantillon de 0,5. Le nombre maximal de nœuds terminaux par arbre est de 6.
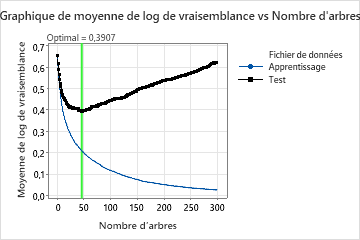
Le graphique Moyenne –Logvraisemblance en fonction du nombre d’arbres montre la courbe entière sur le nombre d’arbres cultivés. La valeur optimale pour les données de test est de 0,3907 lorsque le nombre d’arbres est de 46.
Récapitulatif du modèle
| Nombre total de prédicteurs | 13 |
|---|---|
| Prédicteurs importants | 13 |
| Nombre d'arbres développés | 300 |
| Nombre optimal d'arbres | 46 |
| Statistiques | Apprentissage | Test |
|---|---|---|
| Log de vraisemblance de moyenne | 0,2088 | 0,3907 |
| Zone située sous la courbe ROC | 0,9842 | 0,9032 |
| IC à 95 % | (0,9721; 0,9964) | (0,8683; 0,9381) |
| Lift | 1,8364 | 1,7744 |
| Taux de mauvaise classification | 0,0726 | 0,1520 |
Lorsque le nombre d’arbres est de 46, la table récapitulative du modèle indique que le log-vraisemblance négatif moyen est d’environ 0,21 pour les données d’entraînement et d’environ 0,39 pour les données de test.
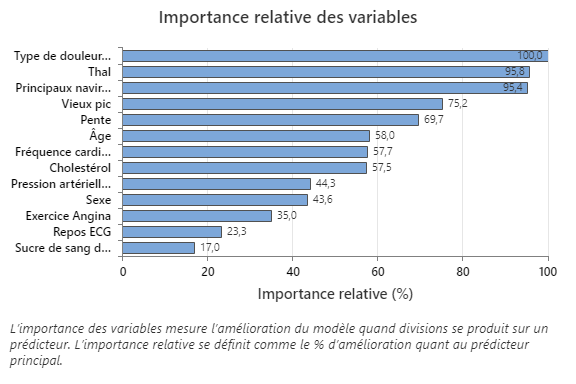
Le graphique Importance relative des variables trace les prédicteurs dans l’ordre de leur effet sur l’amélioration du modèle lorsque des divisions sont effectuées sur un prédicteur au cours de la séquence d’arbres. La variable prédictive la plus importante est le type de douleur thoracique. Si la contribution de la variable prédictive principale, le type de douleur thoracique, est de 100 %, alors la variable importante suivante, Thal, a une contribution de 95,8 %. Cela signifie que Thal est 95,8% aussi important que le type de douleur thoracique dans ce modèle de classification.
Matrice de confusion
| Classe prévue (apprentissage) | |||||||
|---|---|---|---|---|---|---|---|
| Classe prévue (test) | |||||||
| Classe réelle | Dénombrement | 1 | 0 | % correct | 1 | 0 | % correct |
| 1 (Événement) | 165 | 156 | 9 | 94,55 | 147 | 18 | 89,09 |
| 0 | 138 | 13 | 125 | 90,58 | 28 | 110 | 79,71 |
| Tous | 303 | 169 | 134 | 92,74 | 175 | 128 | 84,82 |
| Statistiques | Apprentissage (%) | Test (%) |
|---|---|---|
| Taux de vrai positif (sensibilité ou puissance) | 94,55 | 89,09 |
| Taux de faux positif (erreur de type I) | 9,42 | 20,29 |
| Taux de faux négatif (erreur de type II) | 5,45 | 10,91 |
| Taux de vrai négatif (spécificité) | 90,58 | 79,71 |
La matrice de confusion montre dans quelle mesure le modèle sépare correctement les classes. Dans cet exemple, la probabilité qu’un événement soit prédit correctement est d’environ 89%. La probabilité qu’un non-événement soit prédit correctement est d’environ 80%.
Mauvais classement
| Apprentissage | Test | ||||
|---|---|---|---|---|---|
| Classe réelle | Dénombrement | Mal classé | % erreur | Mal classé | % erreur |
| 1 (Événement) | 165 | 9 | 5,45 | 18 | 10,91 |
| 0 | 138 | 13 | 9,42 | 28 | 20,29 |
| Tous | 303 | 22 | 7,26 | 46 | 15,18 |
Le taux d’erreurs de classification permet d’indiquer si le modèle prédira avec précision les nouvelles observations. Pour la prédiction d’événements, l’erreur de classification du test est d’environ 11 %. Pour la prédiction des non-événements, l’erreur de classification erronée est d’environ 20%. Dans l’ensemble, l’erreur de classification des données de test est d’environ 15%.
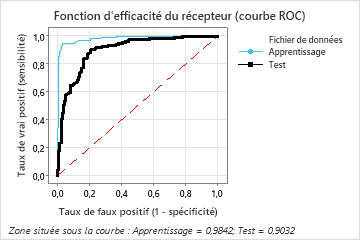
L’aire sous la courbe ROC lorsque le nombre d’arbres est de 46 est d’environ 0,98 pour les données d’entraînement et d’environ 0,90 pour les données d’essai.
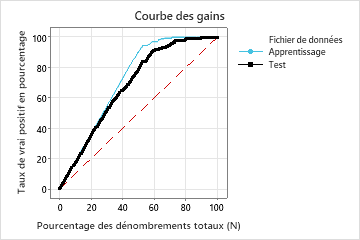
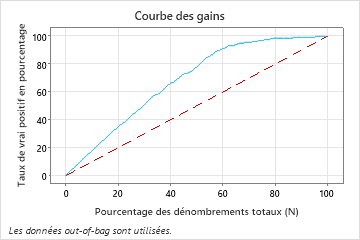
Dans cet exemple, le graphique de gain montre une forte augmentation au-dessus de la ligne de référence, puis un aplatissement. Dans ce cas, environ 60 % des données représentent environ 90 % des vrais positifs. Cette différence est le gain supplémentaire lié à l’utilisation du modèle.
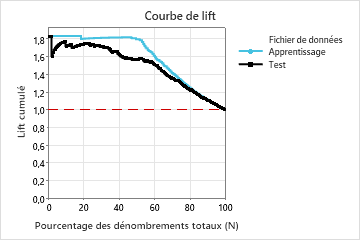
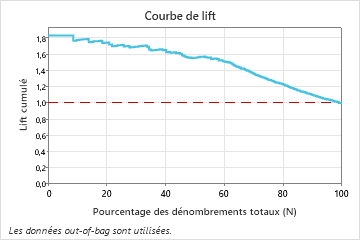
Dans cet exemple, le graphique d’élévation montre une forte augmentation au-dessus de la ligne de référence qui commence à diminuer plus rapidement après environ 50 % du dénombrement total.
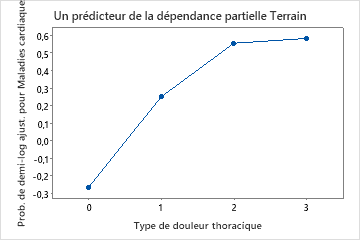
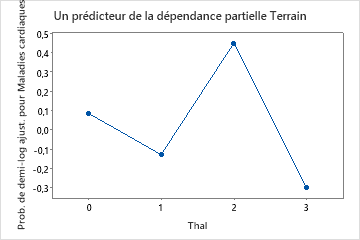
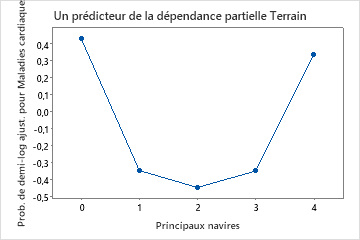
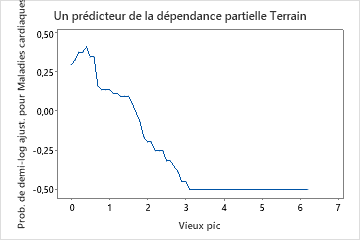
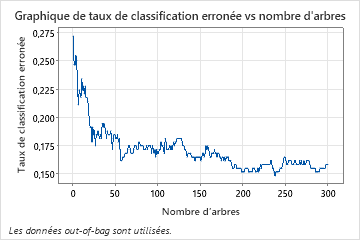
Utilisez les tracés de dépendances partielles pour obtenir des informations sur la façon dont les variables importantes ou les paires de variables affectent les valeurs de réponse ajustées. Les valeurs de réponse ajustées sont sur l’échelle 1/2 log. Les graphiques de dépendance partielle montrent si la relation entre la réponse et une variable est linéaire, monotone ou plus complexe.
Par exemple, dans le graphique de dépendance partielle du type de douleur thoracique, la cote logarithmique de 1/2 est la plus élevée à la valeur de 3. Sélectionnez ou pour produire des tracés pour d’autres variables