Sur ce thème
- Méthodes d'intervalles de tolérance
- Intervalles de tolérance non paramétriques exacts pour les distributions continues
- Loi log-normale
- Intervalles de tolérance approximatifs pour les lois gamma
- Loi exponentielle
- Loi des plus petites valeurs extrêmes
- Loi de Weibull
- Loi des plus grandes valeurs extrêmes
- Loi de distribution logistique
- Loi log-logistique
- Test d'Anderson-Darling
Méthodes d'intervalles de tolérance
- Log-normale
- Gamma
- Exponentielle
- Plus petite valeur extrême
- Weibull
- Plus grande valeur extrême
- Logistique
- Log-logistique
Définitions générales
Soient X 1, X 2, ..., X n les statistiques ordonnées reposant sur un échantillon aléatoire d'effectif n d'une loi de distribution continue.
Soit la fonction de distribution F(x;θ) pour Ω dans un espace de paramètre avec une dimension supérieure ou égale à 1.
Soient L < U deux statistiques basées sur l'échantillon de sorte que pour toutes les valeurs données α et P, avec 0 < α < 1 et 0 < P < 1, la formule suivante est valide pour tous les θ dans Ω :
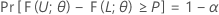
Enfin, l'intervalle [L, U] est un intervalle de tolérance bilatéral avec un contenu égal à P x 100 % et un niveau de confiance égal à 100(1 – α) %. Cet intervalle peut être appelé intervalle de tolérance bilatéral (1 – α, P). Par exemple, si α = 0,10 et que P = 0,85, l'intervalle obtenu est appelé intervalle de tolérance bilatéral (90 %, 0,85).
Si L = –∞ et U < +∞,l'intervalle (-∞, U] est appelé borne de tolérance supérieure unilatérale (1 – α, P). Si L > -∞ et U = +∞, l'intervalle [L, +∞) est appelé borne de tolérance inférieure unilatérale (1 – α, P).
- Une borne de tolérance inférieure unilatérale (1 – α, P) est également une borne de tolérance supérieure unilatérale (P, 1 – α).
- Une borne de confiance inférieure unilatérale (1 – α )100 % du (1 – P)ème percentile de la distribution des données est également une borne de tolérance inférieure unilatérale (1 – α, P). De même, une borne de confiance supérieure unilatérale (1 – α )100 % du P e percentile de la distribution des données est également une borne de tolérance supérieure unilatérale (1 – α , P).
- Si L et U sont des bornes de tolérance inférieure et supérieure unilatérales (1 – α/2 , (1 + P )/2), alors [ L, U ] est une intervalle de tolérance bilatéral approximatif (1 – α, P). Cette méthode peut être utilisée lorsqu'il est impossible d'obtenir directement des intervalles de tolérance bilatéraux. Les intervalles de tolérance bilatéraux qui en résultent sont généralement conservateurs. Voir Guenther1 et Hahn et Meeker2.
- Guenther, W. Montgomery (2004). (1972). Tolerance intervals for univariate distributions. Naval Research Logistics, 19: 309–333.
- Hahn G. J. et Meeker W. Q. (1991). Statistical Intervals: A Guide for Practitioners John Wiley & Sons, New York.
Intervalles de tolérance non paramétriques exacts pour les distributions continues
Minitab calcule les intervalles de tolérance non paramétriques exacts (1 – α, P), où 1 – α représente le niveau de confiance et P représente la couverture (pourcentage minimal cible de la population dans l'intervalle). La méthode non paramétrique pour les intervalles de tolérance est une méthode sans loi de distribution. Cela signifie que l'intervalle de tolérance non paramétrique ne dépend pas de la population parent de l'échantillon. Minitab utilise une méthode exacte à la fois pour les intervalles unilatéraux et bilatéraux.
Soient X 1, X 2 , ... , X n les statistiques ordonnées reposant sur un échantillon aléatoire d'une population distribuée de façon continue F(x;θ). D'après les conclusions de Wilks1, 2 et de Robbins3, il est possible de démontrer ce qui suit :

où B représente la fonction de répartition de la distribution bêta avec les paramètres a = r et b = n – s + 1. Ainsi, ( Xr , Xs ) est un intervalle de tolérance sans distribution car la couverture de l'intervalle présente une distribution bêta avec des valeurs de paramètres connues, qui sont indépendantes de la distribution de la population parente, F(x;θ).
Intervalles unilatéraux
Soit k l'entier le plus grand remplissant la condition suivante :

où Y est une variable aléatoire binomiale avec les paramètres n et 1 – P. Il est possible de démontrer (voir Krishnamoorthy et Mathew4) qu'une borne de tolérance inférieure unilatérale (1 – α, P) est donnée par Xk . De même, une borne de tolérance supérieure unilatérale (1 – α, P) est exprimée par X n - k +1. Dans les deux cas, la couverture réelle ou effective est exprimée par P(Y > k).
Intervalles bilatéraux
Soit k l'entier le plus petit remplissant la condition suivante :

où V est une variable aléatoire binomiale avec les paramètres n et P. Ainsi,
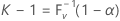
où F V -1(x) représente la fonction de répartition inverse de V. Il est possible de démontrer (voir Krishnamoorthy et Mathew4) qu'un intervalle de tolérance bilatéral (1 – α, P) peut être donné par ( Xr , Xs ). Minitab choisit s = n - r + 1 de sorte que r = ( n – k + 1) / 2. Les deux valeurs r et s sont arrondies à l'entier le plus proche. La couverture réelle ou effective est exprimée par P(V < k – 1).
Notation
| Terme | Description |
|---|---|
| 1 – α | niveau de confiance de l'intervalle de tolérance |
| P | couverture de l'intervalle de tolérance (pourcentage minimal cible de population dans l'intervalle) |
| n | nombre d'observations dans l'échantillon |
- Wilks, S. S. (1941). Sample size for tolerance limits on a normal distribution. The Annals of Mathematical Statistics, 12, 91–96.
- Wilks, S. S. (1941). Statistical prediction with special reference to the problem of tolerance limits. The Annals of Mathematical Statistics, 13, 400–409.
- Robbins, H. (1944). On distribution-free tolerance limits in random sampling. The Annals of Mathematical Statistics, 15, 214–216.
- Krishnamoorthy, K. et Mathew, T. (2009). Statistical Tolerance Regions: Theory, Applications, and Computation. Wiley, Hoboken, NJ.
Loi log-normale
- Minitab prend le logarithme népérien des données.
- Minitab calcule un intervalle de tolérance pour les données transformées en suivant la procédure propre à l'intervalle de tolérance pour la loi normale.
- Minitab élève à la puissance les limites de l'intervalle de tolérance obtenu lors de l'étape précédente pour transformer l'intervalle à l'échelle des données initiales.
Intervalles de tolérance approximatifs pour les lois gamma
L'intervalle de tolérance pour la loi gamma utilise une approximation de la loi normale. Krishnamoorthy et al. mènent des études de simulation qui indiquent que l'approximation fournit des résultats exacts. Les calculs suivent la procédure ci-dessous :
- Minitab prend la racine cubique des données.
- Minitab calcule un intervalle de tolérance pour les données transformées en suivant la procédure propre à l'intervalle de tolérance pour la loi normale.
- Minitab élève à la puissance les limites de l'intervalle de tolérance obtenu lors de l'étape précédente pour transformer l'intervalle à l'échelle des données initiales.
- Krishnamoorthy K., Mathew T et Mukherjee S (2008). Normal based methods for a Gamma distribution: prediction and tolerance intervals and stress-strength reliability. Technometrics, 50, 69—78.
Loi exponentielle
Minitab calcule les intervalles de tolérance exacts (1 – α, P), où 1 – α représente le niveau de confiance et P représente la couverture (proportion minimal cible de la population dans l'intervalle). Les formules diffèrent entre le calcul des limites de tolérance unilatérales et des intervalles de tolérance bilatéraux.
Limites de tolérance exponentielle unilatérales
La formule suivante permet de calculer la limite inférieure :
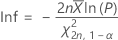
La formule suivante permet de calculer la limite supérieure :
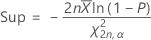
Intervalles de confiance exponentiels bilatéraux
Minitab utilise la méthode de Newton pour résoudre le système d'équations ci-dessous. Pour plus de détails, voir Fernandez1.
La formule suivante permet de calculer l'intervalle bilatéral :

Où

et la valeur de k 1 dépend de la résolution du système d'équations suivant :

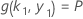
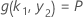
avec
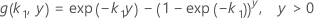
Notation
| Terme | Description |
|---|---|
| n | Effectif de l'échantillon |
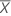 | moyenne de l'échantillon |
| P | proportion minimal cible de la population dans l'intervalle |
 | α e percentile de la loi du Khi deux avec 2n degrés de liberté |
| α | 1 - niveau de confiance |
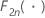 | fonction de répartition de la loi du Khi deux avec 2n degrés de liberté |
- Fernandez, Arturo J. (2010). Two-sided tolerance intervals in the exponential case: Corrigenda and generalizations. Computational Statistics and Data Analysis, 54, 151—162.
Loi des plus petites valeurs extrêmes
Minitab calcule les intervalles de tolérance exacts (1 – α, P) en se basant sur les écrits de Lawless1, où 1 – α représente le niveau de confiance et P représente la couverture (pourcentage minimal cible de la population dans l'intervalle).
Limites de tolérance unilatérales exactes pour les plus petites valeurs extrêmes
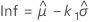
où


avec
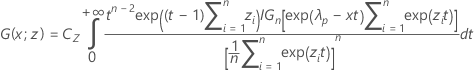
où

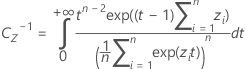
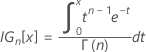
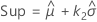
La valeur de k 2 provient du remplacement de α par 1 − α et de P par 1 − P dans les formules permettant de calculer k 1.
Intervalles de tolérance bilatéraux approximatifs pour les plus petites valeurs extrêmes
Pour calculer l'intervalle bilatéral approximatif, remplacez α par α/2 et P par (P + 1)/2 dans les formules permettant de calculer les limites de tolérance unilatérales.
Notation
| Terme | Description |
|---|---|
 | estimation par le maximum de vraisemblance du paramètre d'emplacement pour la loi des valeurs extrêmes |
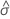 | estimation par le maximum de vraisemblance du paramètre d'échelle pour la loi des valeurs extrêmes |
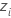 | 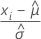 , observations centrées en fonction des estimations EMaxV des paramètres d'emplacement et d'échelle de la loi des plus petites valeurs extrêmes , observations centrées en fonction des estimations EMaxV des paramètres d'emplacement et d'échelle de la loi des plus petites valeurs extrêmes |
| t | α e percentile de la loi T non-centrée avec n − 1 degrés de liberté et le paramètre de non-centralité δP |
| 1 - α | niveau de confiance de l'intervalle de tolérance |
| P | couverture de l'intervalle de tolérance (pourcentage minimal cible de population dans l'intervalle) |
| n | nombre d'observations dans l'échantillon |
- Lawless, J. F. (1975). Construction of tolerance bounds for the extreme-value and the Weibull distribution. Technometrics, 17, 255—261.
Loi de Weibull
- Minitab prend le logarithme népérien des données.
- Minitab calcule un intervalle de tolérance pour les données transformées en suivant la procédure propre à l'intervalle de tolérance pour la loi des plus petites valeurs extrêmes.
- Minitab élève à la puissance les limites de l'intervalle de tolérance obtenu lors de l'étape précédente pour transformer l'intervalle à l'échelle des données initiales.
Loi des plus grandes valeurs extrêmes
- Minitab multiplie les données par −1.
- Minitab calcule une tolérance pour les données transformées en suivant la procédure propre à l'intervalle de tolérance pour la loi des plus petites valeurs extrêmes.
- Minitab élève à la puissance les limites de l'intervalle de tolérance obtenu lors de l'étape précédente pour transformer l'intervalle à l'échelle des données initiales.
Pour les formules qui s'appliquent à la loi des plus petites valeurs extrêmes, reportez-vous à la section relative à cette loi.
Loi de distribution logistique
Minitab calcule des intervalles de tolérance approximatifs (1 − α, P) basés sur Bain et Engelhardt1, où 1 − α est le niveau de confiance et P est la couverture (le pourcentage minimum cible de population dans l’intervalle). La formule du facteur de tolérance inférieur diffère de la formule du facteur de tolérance supérieur.
Limites de tolérance logistique unilatérales
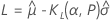
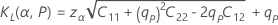
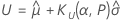
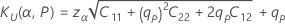
Intervalles de tolérance logistique bilatéraux
L’analyse produit un intervalle de tolérance bilatéral approximatif pour la distribution logistique avec l’inégalité de Bonferroni2. Cette méthode d’approximation remplace α par α/2 et P par ( P + 1)/2 dans les formules de calcul des limites de tolérance unilatérales.
Notation
| Terme | Description |
|---|---|
 | le facteur de tolérance plus faible |
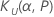 | le facteur de tolérance supérieur |
| zα | le α centile supérieur de la distribution normale standard, qui est équivalent au point inférieur de 1 − α percentile |
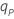 | log(p) − log(1 − p ), le p× 100 percentile inférieur de la distribution logistique standard |
| C11 | 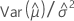 |
| C22 |  |
| C12 | 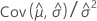 |
 | estimation par le maximum de vraisemblance du paramètre d'emplacement logistique |
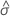 | estimation par le maximum de vraisemblance du paramètre d'échelle logistique |
- Bain, L. and Englehardt, M. (1991). Statistical analysis of reliability and life testing models: Theory and methods. Second edition, Marcel Dekker, Inc.
- Hahn, G. J. and Meeker, W. Q. (2017). Statistical intervals: A guide for practitioners. Second edition, John Wiley and Sons, Inc.
Loi log-logistique
- Minitab prend le logarithme népérien des données.
- Minitab calcule un intervalle de tolérance pour les données transformées en suivant la procédure propre à l'intervalle de tolérance pour la loi logistique.
- Minitab élève à la puissance les limites de l'intervalle de tolérance obtenu lors de l'étape précédente pour transformer l'intervalle à l'échelle des données initiales.
Pour les formules qui s'appliquent à la loi logistique, reportez-vous à la section relative à cette loi.
Test d'Anderson-Darling
Minitab utilise les statistiques d'Anderson-Darling pour effectuer le test d'adéquation de l'ajustement.
Soit Z = F(X), où F(X) représente la fonction de répartition. Supposons qu'un échantillon X1, .., Xn donne les valeurs Z(i) = F(Xi), i=1,.., n. Triez Z(i) par ordre croissant, Z(1) < Z(2) <...<Z(n). La statistique d'Anderson-Darling (A2) isest alors calculée comme suit :
- A2 = –n - (1/n) Σi[(2i – 1) log Z(i) + (2n + 1 – 2i) log (1 – Z(i))]
La statistique du test d'adéquation de l'ajustement d'Anderson-Darling modifiée est calculée pour chaque loi. Les valeurs de p sont basées sur le tableau présenté par D'Agostino et Stephens.1 Si le tableau ne contient aucune valeur de p exacte, Minitab calcule la valeur de p basée sur l'interpolation à l'aide de l'étendue de la valeur de p.
