Sur ce thème
DL
Degrés de liberté (DL) pour chaque SC (somme des carrés). En règle générale, le DL mesure la quantité d'informations disponible pour le calcul de chaque SC.
Somme des carrés
La somme des carrés (SC) est la somme des distances quadratiques. Il s'agit d'une mesure de la variabilité issue de différentes sources. La somme des carrés totale indique la variabilité des données par rapport à la moyenne globale. La somme des carrés de l'opérateur indique la variabilité entre la mesure moyenne pour chaque opérateur et la moyenne globale.
SomCar totale = SomCar Pièce + SomCar Opérateur + SomCar Opérateur*Pièce + SomCar Répétabilité
CM
Les carrés moyens (CM) correspondent à la variabilité des données issue de différentes sources. La méthode des carrés moyens tient compte du fait que des sources différentes ont des nombres différents de niveaux ou de valeurs possibles.
CM = SomCar/DL pour chaque source de variabilité
F
La statistique F permet de déterminer si les effets des termes Opérateur, Pièce ou Opérateur*Pièce sont statistiquement significatifs.
Plus la statistique F est élevée, plus il est probable que le facteur contribue significativement à la variabilité de la variable de mesure ou de réponse.
P
La valeur de p correspond à la probabilité d'obtenir une statistique de test (telle qu'une statistique F) au moins aussi extrême que la valeur que vous avez calculée à partir de l'échantillon, si l'hypothèse nulle est vérifiée.
Interprétation
Utilisez la valeur de p dans le tableau ANOVA pour déterminer si les mesures moyennes sont significativement différentes. Minitab affiche un tableau ANOVA seulement si vous sélectionnez l'option ANOVA pour Méthode d'analyse.
Une valeur de p faible indique que l'hypothèse selon laquelle l'ensemble des pièces, des opérateurs ou des interactions partagent la même moyenne n'est probablement pas vraie.
- Valeur de p ≤ α : au moins une moyenne est statistiquement différente
- Si la valeur de p est inférieure ou égale au seuil de signification, vous rejetez l'hypothèse nulle et concluez qu'au moins une des moyennes est significativement différente des autres. Par exemple, au moins un opérateur mesure différemment.
- Valeur de p > α : les moyennes ne sont pas significativement différentes.
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle car vous ne possédez pas suffisamment de preuves pour conclure que les moyennes de la population sont différentes. Par exemple, vous ne pouvez pas conclure que les opérateurs mesurent différemment.
CompVar
CompVar est l'estimation de composante de variance pour chaque source dans un tableau ANOVA.
Interprétation
Les composantes de la variance permettent d'évaluer la variation pour chaque source d'erreur de mesure.
Dans un système de mesure acceptable, la plus grande composante de variation est la variation de pièce à pièce. Si la répétabilité et la reproductibilité contribuent largement à la variation, vous devez examiner la source du problème et prendre des mesures correctives.
% contribution (de CompVar)
La valeur % contribution est le pourcentage de variation globale issue de chaque composante de variance. Elle est calculée comme la composante de la variance pour chaque source, divisée par la variation totale, puis multipliée par 100 pour être exprimée en pourcentage.
Interprétation
Utilisez la valeur % contribution pour évaluer la variation de chaque source d'erreur de mesure.
Dans un système de mesure acceptable, la plus grande composante de variation est la variation de pièce à pièce. Si la répétabilité et la reproductibilité contribuent largement à la variation, vous devez examiner la source du problème et prendre des mesures correctives.
Ecart type
Ecart type de chaque source de variation. L'écart type est égal à la racine carrée de la composante de variance pour cette source.
L'écart type est une mesure pratique de la variation car il utilise les mêmes unités que les mesures de pièces et la tolérance.
Variations d’étude (6 * écart type)
La variation de l'étude est calculée comme l'écart type de chaque source de variation multiplié par 6 ou par le multiplicateur indiqué dans Variation de l'étude.
En général, la variation de procédé est définie comme 6e, e correspondant à l'écart type sous forme d'estimation de l'écart type de la population (noté σ ou sigma). Lorsque les données sont distribuées normalement, environ 99,73 % des données se situent à moins de 6 écarts types de la moyenne. Pour définir un pourcentage de données différent, utilisez un autre multiplicateur de l'écart type. Par exemple, si vous souhaitez savoir où se situent 99 % des données, vous utiliserez un multiplicateur de 5,15, plutôt que le multiplicateur par défaut de 6.
% var étude (%VE)
La valeur %Variation de l'étude est calculée comme la variation de l'étude pour chaque source de variation, divisée par la variation totale et multipliée par 100.
La valeur Var. de l'étude (%) est la racine carrée de la composante de la variance calculée (CompVar) pour cette source. Ainsi, la somme des valeurs % contribution de CompVar est égale à 100, contrairement aux valeurs Var. de l'étude (%).
Interprétation
Utilisez la fonctionnalité % var étude pour comparer la variation du système de mesure à la variation totale. Si vous utilisez le système de mesure pour évaluer les améliorations de procédé, notamment la réduction de la variation de pièce à pièce, % var étude est une meilleure estimation de la précision de mesure. Si vous souhaitez évaluer la capabilité du système de mesure pour évaluer des pièces par rapport à la spécification, % tolérance est la mesure appropriée.
% tolérance (VE/Tolér.)
La valeur % Tolérance est calculée comme suit : variation de l'étude pour chaque source, divisée par la tolérance de procédé et multipliée par 100.
Si vous entrez la tolérance, Minitab calcule la valeur % Tolérance, qui compare la variation du système de mesure aux spécifications.
Interprétation
Utilisez la valeur % Tolérance pour évaluer les pièces par rapport aux spécifications. Si vous utilisez le système de mesure pour l'amélioration du procédé, notamment la réduction de la variation de pièce à pièce, % Var étude est la mesure appropriée.
% procédé (VE/Proc)
Si vous indiquez un écart type historique, mais utilisez les pièces de l'étude pour estimer la variation de procédé, Minitab calcule la valeur %Procédé. Cette valeur compare la variation du système de mesure à la variation historique du procédé. La valeur %Procédé est calculée de la façon suivante : variation de l'étude pour chaque source, divisée par la variation historique du procédé et multipliée par 100. Par défaut, la variation du procédé est égale à 6 fois l'écart type historique.
Si vous utilisez un écart type historique pour estimer la variation de procédé, Minitab n'affiche pas la valeur %Procédé car elle est identique à la valeur %Var. de l'étude.
IC à 95 %
Les intervalles de confiance à 95 % (IC à 95 %) sont des étendues de valeurs susceptibles de contenir la valeur réelle de chaque évaluation d'erreur de mesure.
Minitab fournit des intervalles de confiance pour les composantes de la variance, la valeur % contribution des composantes de la variance, l'écart type, la variation de l'étude, la valeur %Variation de l'étude, la valeur %Tolérance et le nombre de catégories distinctes.
Interprétation
Les échantillons de données étant aléatoires, il est peu probable que deux études de l'instrumentation donnent des intervalles de confiance identiques. Cependant, si vous répétez vos études de nombreuses fois, un certain pourcentage d'intervalles de confiance obtenus contiendra l'erreur de mesure réelle inconnue. Le pourcentage de ces intervalles de confiance contenant le paramètre est le niveau de confiance de l'intervalle.
Par exemple, avec un niveau de confiance de 95 %, vous pouvez être sûr à 95 % que l'intervalle de confiance comprend la valeur réelle. L'intervalle de confiance vous aide à évaluer la signification pratique de vos résultats. Utilisez vos connaissances spécialisées pour déterminer si l'intervalle de confiance comporte des valeurs ayant une signification pratique pour votre situation. Si l'intervalle est trop grand pour être utile, envisagez d'augmenter votre effectif d'échantillon.
Supposons que la composante de la variance pour Répétabilité soit de 0,044727 et que l'IC à 95 % correspondant soit de (0,035, 0,060). L'estimation de la variation de la répétabilité est calculée à partir des données comme étant égale à 0,044727. Vous pouvez être sûr à 95 % que l'intervalle allant de 0,035 à 0,060 contient la variation réelle de la répétabilité.
Nombre de catégories distinctes
Le nombre de catégories distinctes est une mesure utilisée dans les études de R&R de l'instrumentation afin d'identifier la capacité d'un système de mesure à détecter une différence dans la caractéristique mesurée. Le nombre de catégories distinctes représente le nombre d'intervalles de confiance non superposés qui recouvrent l'étendue de la variation du produit examiné, selon la définition des échantillons choisis. Le nombre de catégories distinctes représente également le nombre de groupes que votre système de mesure peut distinguer dans les données du procédé.
Interprétation
Le manuel Measurement Systems Analysis1 publié par l'Automobile Industry Action Group (AIAG), stipule qu'au moins 5 catégories indiquent un système de mesure acceptable. Si le nombre de catégories distinctes est inférieur à 5, la résolution du système de mesure peut être insuffisante.
En règle générale, lorsque le nombre de catégories distinctes est inférieur à 2, le système de mesure ne présente aucun intérêt pour le contrôle du procédé, car il est impossible de différencier une pièce d'une autre. Lorsque le nombre de catégories distinctes est égal à 2, il est possible de diviser les pièces en 2 groupes : haut et bas. Lorsque le nombre de catégories distinctes est égal à 3, il est possible de diviser les pièces en 3 groupes : haut, moyen et bas.
Pour plus d'informations, accédez à la rubrique Utilisation du nombre de catégories distinctes.
Probabilités de mauvais classement
Lorsque vous indiquez au moins une limite de spécification, Minitab peut calculer les probabilités de mauvais classement d'un produit. Etant donné la variation d'instrumentation, la valeur mesurée de la pièce n'est pas toujours égale à sa valeur réelle. L'écart entre la valeur mesurée et la valeur réelle crée une possibilité de mauvais classement de la pièce.
- Probabilité conjointe
- Utilisez la probabilité conjointe lorsque vous ne possédez pas de connaissances préalables sur le caractère acceptable des pièces. Prenons l'exemple d'un échantillon prélevé dans une chaîne de production sans que vous sachiez si telle ou telle pièce est de bonne ou de mauvaise qualité. Vous pouvez effectuer un mauvais classement de deux façons :
- Probabilité que la pièce soit mauvaise et que vous l'acceptiez.
- Probabilité que la pièce soit bonne et que vous la rejetiez.
- Probabilité conditionnelle
- Utilisez l'option Probabilité conditionnelle lorsque vous possédez des connaissances préalables sur le caractère acceptable des pièces. Prenons l'exemple d'un échantillon prélevé dans une pile de pièces à réusiner ou dans une pile de produits prêts à être expédiés et considérés comme étant de bonne qualité. Vous pouvez effectuer un mauvais classement de deux façons :
- Probabilité que vous acceptiez une pièce échantillonnée dans une pile de mauvais produits devant être réusinés (également appelée acceptation à tort).
- Probabilité que vous rejetiez une pièce échantillonnée dans une pile de bons produits sur le point d'être expédiés (également appelée rejet à tort).
Interprétation
Probabilité conjointe
| Description | Probabilité |
|---|---|
| Une pièce sélectionnée de manière aléatoire est incorrecte mais acceptée | 0,037 |
| Une pièce sélectionnée de manière aléatoire est correcte mais rejetée | 0,055 |
Probabilité conditionnelle
| Description | Probabilité |
|---|---|
| Une pièce d'un groupe de produits incorrects est acceptée | 0,151 |
| Une pièce d'un groupe de produits corrects est rejetée | 0,073 |
La probabilité conjointe qu'une pièce soit mauvaise et que vous l'acceptiez est de 0,037. La probabilité conjointe qu'une pièce soit bonne et que vous la rejetiez est de 0,055.
La probabilité conditionnelle d'une acceptation à tort, c'est-à-dire que vous acceptiez une pièce pendant la réinspection alors qu'elle est en réalité hors spécification, est de 0,151. La probabilité conditionnelle d'un rejet à tort, c'est-à-dire que vous rejetiez une pièce pendant la réinspection alors qu'elle est en réalité dans les spécifications, est de 0,073.
VDA 5
Remarque
VDA 5 est uniquement dans l’application web.
Remarque
L’analyse utilise l’incertitude maximale entre uEVR, uRE et uEVO pour calculer la variation du processus de mesure. Le % du total pour les 2 autres statistiques est manquant car ces statistiques ne contribuent pas au total.
- Étalonnage (uCAL)
- L’étalonnage (uCAL) est l’incertitude des mesures résultant de l’étalonnage de l’étalon de référence. Cette statistique est un intrant de l’analyse. Habituellement, cette valeur provient du certificat d’étalonnage.
- Répétabilité à la référence (uEVR)
- La répétabilité à la référence (uEVR) est l’incertitude résultant des mesures répétées de la pièce de référence par le même opérateur avec le même appareil. Cette statistique est un intrant de l’analyse. Habituellement, cette valeur provient d’une étude de jauge de type I.
- Résolution (uRE)
- La résolution (uRE) est l’incertitude due à la résolution de la jauge. L’analyse calcule cette statistique lorsque la résolution de la jauge est une entrée de l’analyse.
- Répétabilité de l’objet mesuré (uEVO)
- La répétabilité de l’objet mesuré (uEVO) est l’incertitude due à la répétabilité dans l’étude Gage R&R. La répétabilité est la variabilité des mesures lorsqu’un même opérateur mesure plusieurs fois la même pièce.
- Biais (uBI)
- Le biais (uBI) est l’incertitude dans les mesures due à la différence entre la mesure de référence connue et la moyenne des mesures de l’étude. Cette statistique est un intrant de l’analyse. Habituellement, cette valeur provient d’une étude de biais où la pièce de référence se trouve dans la plage des mesures.
- Linéarité (uLIN)
- La linéarité (uLIN) est l’incertitude des mesures dues à la linéarité. La linéarité est la différence entre la valeur de la pièce de référence et la mesure moyenne qui provient de la variation du biais lorsque la valeur de la pièce change. Cette statistique est un intrant de l’analyse. Habituellement, cette valeur provient d’une étude de linéarité où la pièce de référence se trouvait dans la plage de mesures.
- Autres facteurs (uREST)
- Les autres facteurs (uREST) sont l’incertitude dans les mesures due à un ou plusieurs facteurs supplémentaires. Si les spécifications de l’analyse comportent un facteur supplémentaire, alors cette incertitude est un intrant de l’analyse. Si les spécifications de l’analyse comportent plus d’un facteur, cette incertitude combine les valeurs. Par exemple, utilisez les spécifications pour d’autres facteurs afin de tenir compte de l’incertitude due à la température si les mesures présentent des différences plus importantes lorsque la collecte de données se déroule à une température plus élevée.
- Opérateurs (uAV)
- Opérateurs (uAV) est l’incertitude dans les mesures due à la reproductibilité dans l’étude R&R de l’instrumentation. La reproductibilité est la variabilité des mesures lorsque différents opérateurs mesurent la même pièce.
- Interactions (uIA)
- Les interactions (uIA) sont l’incertitude dans les mesures due à l’interaction entre la pièce et l’opérateur dans l’étude R&R de l’instrumentation. L’interaction a lieu dans l’analyse lorsque l’interaction Pièce/Opérateur est statistiquement significative dans la table ANOVA.
- Processus de mesure (uMP)
- Le processus de mesure (uMP) combine toutes les composantes d’incertitude pour estimer l’incertitude totale du processus de mesure.
- % du total
- Pour chaque source d’incertitude, l’analyse présente le pourcentage de l’uMP qui résulte de cette source. Utilisez le pourcentage pour comparer le degré d’incertitude provenant des différentes sources.
- % de tolérance ( %QMP)
- Le % de tolérance ( %QMP) combine l’incertitude du processus de mesure avec la variation de l’étude et compare la valeur à la tolérance du processus. %QMP est un moyen courant de décider si un processus de mesure est satisfaisant. Dans certaines applications, une valeur de 30 % ou moins indique qu’un processus de mesure est satisfaisant.
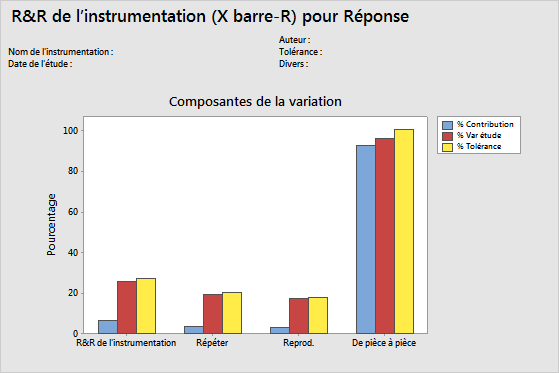
Graphique Composantes de la variation
Les composantes de la carte de variation constituent le récapitulatif graphique des résultats d'une étude de R&R de l'instrumentation.
- R&R de l'instrumentation totale : variabilité issue du système de mesure qui inclut plusieurs opérateurs à l'aide de la même instrumentation.
- Répétabilité : variabilité des mesures lorsque la même pièce est mesurée plusieurs fois par le même opérateur.
- Reproductibilité : variabilité des mesures lorsque la même pièce est mesurée par plusieurs opérateurs.
- De pièce à pièce : variabilité des mesures due aux différentes pièces.
Interprétation
- % contribution
- La valeur %Contribution est le pourcentage de variation globale issue de chaque composante de variance. Elle est calculée comme la composante de la variance pour chaque source, divisée par la variation totale, puis multipliée par 100.
- %Variation de l'étude
- La valeur %Variation de l'étude représente le pourcentage de variation de l'étude issue de chaque source. Elle est calculée comme la variation de l'étude pour chaque source, divisée par la variation totale et multipliée par 100.
- %Tolérance
- La valeur %Tolérance compare la variation du système de mesure aux spécifications. Elle est calculée comme la variation de l'étude pour chaque source, divisée par la tolérance de procédé et multipliée par 100.
- % du procédé
- La valeur % du procédé compare la variation du système de mesure à la variation totale. Elle est calculée comme la variation de l'étude pour chaque source, divisée par la variation historique du procédé et multipliée par 100.
Dans un système de mesure acceptable, la plus grande composante de variation est la variation de pièce à pièce.
Carte R
La carte R est une carte de contrôle des étendues qui représente la cohérence des opérateurs.
- Points relevés
- Pour chaque opérateur, il s'agit de la différence entre les mesures minimales et maximales sur chaque pièce. La carte R représente les points par opérateur ; par conséquent, vous pouvez juger de la cohérence de chaque opérateur.
- Ligne centrale (R barre)
- Moyenne générale pour le procédé (c'est-à-dire, moyenne de toutes les étendues d'échantillon).
- Limites de contrôle (LCI et LCS)
- Degré de variation auquel vous pouvez vous attendre pour les étendues d'échantillon. Pour calculer les limites de contrôle, Minitab utilise la variation à l'intérieur des échantillons.
Remarque
Si chaque opérateur mesure chaque pièce au moins 9 fois, Minitab affiche une carte S au lieu d'une carte R.
Interprétation
Lorsque l'étendue moyenne est petite, le système de mesure présente une faible variation. Un point situé au-delà de la limite de contrôle supérieure (LCS) indique que l'opérateur ne mesure pas les pièces de façon cohérente. Le calcul de la LCS inclut le nombre de mesures par pièce et par opérateur, ainsi que la variation de pièce à pièce. Si les opérateurs mesurent les pièces de façon cohérente, l'étendue entre les mesures les plus hautes et les plus basses est faible par rapport à la variation de l'étude et les points sont maîtrisés.
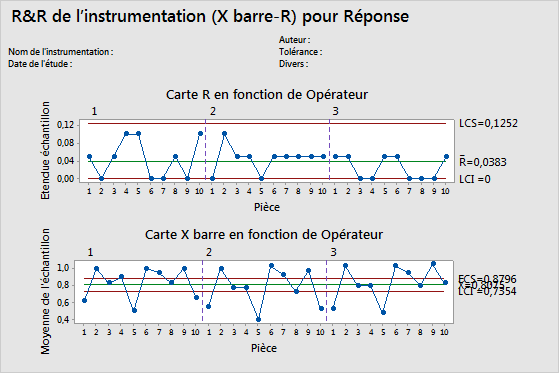
Carte X barre
La carte X barre compare la variation de pièce à pièce à la composante de répétabilité.
- Points relevés
- Mesure moyenne de chaque pièce, représentée par chaque opérateur.
- Ligne centrale (X barre)
- Moyenne globale de toutes les mesures des pièces par tous les opérateurs.
- Limites de contrôle (LCI et LCS)
- Les limites de contrôle sont basées sur l'estimation de répétabilité et sur le nombre de mesures dans chaque moyenne.
Interprétation
Les pièces choisies pour une étude de R&R de l'instrumentation doivent représenter l'étendue entière de pièces possibles. Ainsi, ce graphique doit indiquer une variation entre les moyennes de pièces supérieure à celle qui est attendue de la variation de répétabilité seule.
L'idéal est que le graphique possède des limites de contrôle étroites avec de nombreux points hors contrôle indiquant un système de mesure avec une faible variation.

Graphique Par pièce
Ce graphique affiche les différences entre les niveaux de facteurs. Les études de R&R de l'instrumentation classent habituellement les mesures par pièce et par opérateur. Cependant, une étude de R&R de l'instrumentation permet de représenter d'autres facteurs sur le graphique.
Dans ce graphique, les points et les cercles croisés représentent respectivement les mesures et les moyennes. La ligne de jonction relie les mesures moyennes pour chaque niveau de facteur.
Remarque
S'il existe plus de 9 observations par niveau, Minitab affiche une boîte à moustaches plutôt qu'un diagramme des valeurs individuelles.
Interprétation
Plusieurs mesures pour chaque pièce individuelle qui varient le plus faiblement possible (les points d'une pièce sont proches) indiquent que le système de mesure présente une légère variation. En outre, les mesures moyennes des pièces doivent varier suffisamment pour montrer que les pièces sont différentes et représenter l'ensemble de l'étendue du procédé.
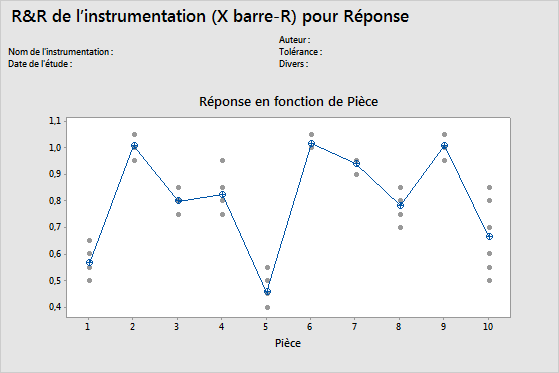
Graphique Par opérateur
Le graphique Par opérateur indique toutes les mesures prises au cours de l'étude, classées par opérateur. Ce graphique affiche les différences entre les niveaux de facteurs. Les études de R&R de l'instrumentation classent habituellement les mesures par pièce et par opérateur. Cependant, une étude de R&R de l'instrumentation permet de représenter d'autres facteurs sur le graphique.
Remarque
S'il existe moins de 10 observations par opérateur, Minitab affiche un diagramme des valeurs individuelles plutôt qu'une boîte à moustaches.
Interprétation
Une ligne droite horizontale entre les opérateurs indique que les mesures moyennes pour chaque opérateur sont similaires. L'idéal est que les mesures de chaque opérateur varient de façon similaire.
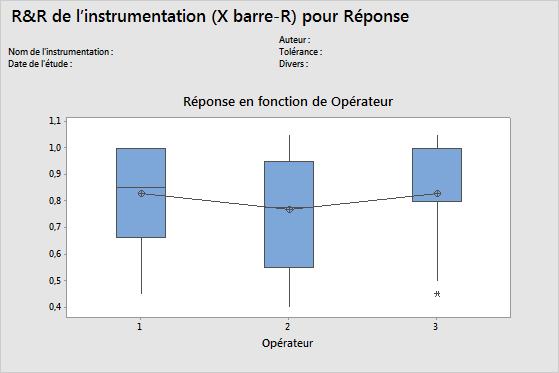
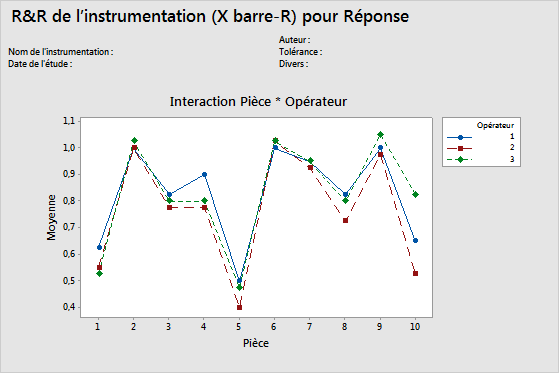
Diagramme des interactions Opérateur*Pièce
Le diagramme des interactions Opérateur*Pièce affiche les mesures moyennes effectuées par chaque opérateur pour chaque pièce. Chaque ligne relie les moyennes pour un seul opérateur (ou pour un terme que vous indiquez).
Les diagrammes des interactions affichent l'interaction entre deux facteurs. Une interaction survient lorsque l'effet d'un facteur dépend d'un autre facteur. Ce diagramme est graphiquement analogue au test F pour un terme d'interaction dans le tableau ANOVA.
Interprétation
Les lignes qui coïncident indiquent que les opérateurs mesurent de façon similaire. Les lignes qui ne sont pas parallèles ou qui se croisent indiquent que la capacité d'un opérateur à mesurer une pièce dépend invariablement de la pièce mesurée. Une ligne qui est invariablement supérieure ou inférieure aux autres indique qu'un opérateur ajoute un biais à la mesure en sous-estimant ou en surestimant invariablement.